ΧβΡΩΡΎ»ί
12Θ°Θ®1Θ©»γΆΦΔΌΘ§AB «Γ―OΒΡœ“Θ§ΒψC «Γ―O…œΒΡ“ΜΒψΘ§‘Ύ÷±œΏAB…œΖΫ’““ΜΒψDΘ§ ΙΒΟΓœADB=ΓœACBΘ§Μ≠≥ωΓœADBΘ§≤ΔΥΒΟςάμ”…ΘΜΘ®2Θ©»γΆΦΔΎΘ§AB «Γ―OΒΡœ“Θ§ΒψC «Γ―O…œΒΡ“ΜΒψΘ§‘ΎΙΐΒψCΒΡ÷±œΏl…œ’““ΜΒψPΘ§ ΙΒΟΓœAPBΘΦΓœACBΘ§Μ≠≥ωΓœAPBΘ§≤ΔΥΒΟςάμ”…ΘΜ
Έ ΧβΫβΨωΘΚ
Θ®3Θ©»γΆΦΔέΘ§“―÷ΣΉψ«ρ«ρΟ≈ΩμAB‘ΦΈΣ5$\sqrt{2}$ΟΉΘ§“Μ«ρ‘±¥”ΨύBΒψ5$\sqrt{2}$ΟΉΒΡCΒψΘ®ΒψAΓΔBΓΔCΨυ‘Ύ«ρ≥ΓΒΉœΏ…œΘ©Θ§―Ί”κAC≥…45ΓψΫ«ΒΡCDΖΫœρ¥χ«ρΘ° ‘Έ Θ§ΗΟ«ρ‘±ΡήΖώ‘Ύ…δœΏCD…œ’“ΒΫ“ΜΒψPΘ§ ΙΒΟΒψPΈΣΉνΦ―…δΟ≈ΒψΘ®Φ¥ΓœAPBΉν¥σΘ©ΘΩ»τΡή’“ΒΫΘ§«σ≥ω’β ±ΒψP”κΒψCΒΡΨύάκΘΜ»τ’“≤ΜΒΫΘ§«κΥΒΟςάμ”…Θ°
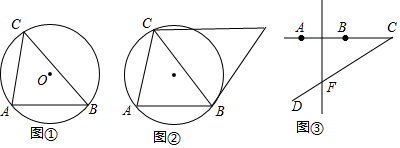
Ζ÷Έω Θ®1Θ©‘Ύ”≈ΜΓAB…œ»Έ“β»Γ“ΜΒψDΘ§Ν§Ϋ”ADΓΔBDΘ§‘ρΓœADB=ΓœACBΘ°ΗυΨίΆ§ΜΓΥυΕ‘ΒΡ‘≤÷ήΫ«œύΒ»Φ¥Ω…÷ΛΟςΘ°
Θ®2Θ©»γΆΦΔΎ÷–Θ§ΙΐΒψCΒΡ÷±œΏl”κΓ―OΫΜ”ΎΒψEΘ§‘ΎCEΒΡ―”≥ΛœΏ…œ»Γ“ΜΒψPΘ§Ν§Ϋ”PAΓΔPBΘ§‘ρΓœAPBΘΦΓœACBΘ°…ηAPΫΜΓ―O”ΎFΘ°”…ΓœAFBΘΨΓœAPBΘ§ΓœAFB=ΓœACBΘ§Φ¥Ω…÷ΛΟςΘ°
Θ®3Θ©»γΆΦΔέ÷–Θ§ΉςΨ≠ΙΐΒψAΓΔB«“ΚΆ÷±œΏCDœύ«–ΒΡ‘≤Θ§«–ΒψΈΣPΘ§¥Υ ±ΓœAPBΉν¥σΘ°ΗυΨί«–œΏ≥ΛΕ®άμΦ¥Ω…ΦΤΥψΘ°
Ϋβ¥π ΫβΘΚΘ®1Θ©»γΆΦΔΌ÷–Θ§
‘Ύ”≈ΜΓAB…œ»Έ“β»Γ“ΜΒψDΘ§Ν§Ϋ”ADΓΔBDΘ§‘ρΓœADB=ΓœACBΘ°
άμ”…ΘΚΓΏ$\widehat{AB}$=$\widehat{AB}$Θ§
ΓύΓœADB=ΓœACBΘ°
Θ®2Θ©»γΆΦΔΎ÷–Θ§ΙΐΒψCΒΡ÷±œΏl”κΓ―OΫΜ”ΎΒψEΘ§‘ΎCEΒΡ―”≥ΛœΏ…œ»Γ“ΜΒψPΘ§Ν§Ϋ”PAΓΔPBΘ§‘ρΓœAPBΘΦΓœACBΘ°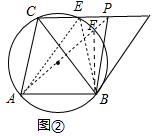
άμ”…ΘΚ…ηAPΫΜΓ―O”ΎFΘ°
ΓΏΓœAFBΘΨΓœAPBΘ§ΓœAFB=ΓœACBΘ§
ΓύΓœAPBΘΦΓœACBΘ°
Θ®3Θ©»γΆΦΔέ÷–Θ§ΉςΨ≠ΙΐΒψAΓΔB«“ΚΆ÷±œΏCDœύ«–ΒΡ‘≤Θ§«–ΒψΈΣPΘ§¥Υ ±ΓœAPBΉν¥σΘ°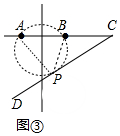
ΓΏPC ««–œΏΘ§
ΓύPC2=CB•CAΘ§Θ®Ω…“‘÷ΛΟςΓςCPBΓΉΓςCAPΘ§ΒΟΒΫ$\frac{CP}{CA}$=$\frac{CB}{CP}$Θ©
ΓΏCB=5$\sqrt{2}$Θ§AC=10$\sqrt{2}$Θ§
ΓύPC2=5$\sqrt{2}$ΓΝ10$\sqrt{2}$=100Θ§
ΓύPC=10ΟΉΘ§
¥πΘΚΒψP”κΒψCΒΡΨύάκΈΣ10ΟΉΘ°
ΒψΤά ±ΨΧβΩΦ≤ι‘≤ΉέΚœΧβΓΔΆ§ΜΓΥυΕ‘ΒΡ‘≤÷ήΫ«œύΒ»ΓΔ«–œΏ≥ΛΕ®άμΓΔ»ΐΫ«–ΈΒΡΆβΫ«¥σ”Ύ»ΈΚΈ“ΜΗω≤ΜœύΝΎΒΡΡΎΫ«Β»÷Σ ΕΘ§ΫβΧβΒΡΙΊΦϋ «―ßΜαΧμΦ”≥Θ”ΟΗ®÷ζœΏΘ§ τ”Ύ÷–ΩΦ≥ΘΩΦΧβ–ΆΘ°

| AΘ° | $\sqrt{Θ®-4Θ©ΓΝΘ®-9Θ©}$=$\sqrt{-4}$ΓΝ$\sqrt{-9}$=6 | BΘ° | Θ®$\sqrt{3}$-1Θ©2=3-1=2 | ||
| CΘ° | $\sqrt{4{1}^{2}-4{0}^{2}}$=$\sqrt{81}$ΓΝ$\sqrt{1}$=9 | DΘ° | 3$\sqrt{\frac{2}{3}}$=$\sqrt{2}$ |
| AΘ° | $\frac{1}{2}$ | BΘ° | 2 | CΘ° | -2 | DΘ° | -$\frac{1}{2}$ |
| AΘ° | 100cm2 | BΘ° | 200cm2 | CΘ° | 300cm2 | DΘ° | 400cm2 |
| AΘ° | sinA=cosB | BΘ° | sinA=sinB | CΘ° | cosA=cosB | DΘ° | sinB=cosB |
 »γΆΦΘ§ ΐ÷α…œœΏΕΈAB=2Θ§CD=4Θ§ΒψA‘Ύ ΐ÷α…œ±μ ΨΒΡ ΐ «-10Θ§ΒψC‘Ύ ΐ÷α…œ±μ ΨΒΡ ΐ «16Θ§»τœΏΕΈAB“‘6ΗωΒΞΈΜ/ΟκΒΡΥΌΕ»œρ”“‘»ΥΌ‘ΥΕ·Θ§Ά§ ±œΏΕΈCD“‘2ΗωΒΞΈΜ/ΟκΒΡΥΌΕ»œρΉσ‘»ΥΌ‘ΥΕ·Θ°
»γΆΦΘ§ ΐ÷α…œœΏΕΈAB=2Θ§CD=4Θ§ΒψA‘Ύ ΐ÷α…œ±μ ΨΒΡ ΐ «-10Θ§ΒψC‘Ύ ΐ÷α…œ±μ ΨΒΡ ΐ «16Θ§»τœΏΕΈAB“‘6ΗωΒΞΈΜ/ΟκΒΡΥΌΕ»œρ”“‘»ΥΌ‘ΥΕ·Θ§Ά§ ±œΏΕΈCD“‘2ΗωΒΞΈΜ/ΟκΒΡΥΌΕ»œρΉσ‘»ΥΌ‘ΥΕ·Θ°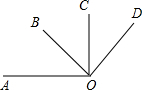 »γΆΦΘ§»τΓœAOD=120ΓψΘ§ΓœBOC=70ΓψΘ§«“ΓœAOCΘΚΓœBOD=9ΘΚ10Θ§‘ρΓœAOB=20ΓψΘ°
»γΆΦΘ§»τΓœAOD=120ΓψΘ§ΓœBOC=70ΓψΘ§«“ΓœAOCΘΚΓœBOD=9ΘΚ10Θ§‘ρΓœAOB=20ΓψΘ°