题目内容
13.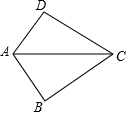 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )| A. | CB=CD | B. | ∠BCA=∠DCA | C. | ∠BAC=∠DAC | D. | ∠B=∠D=90° |
分析 由图形可知AC=AC,结合全等三角形的判定方法逐项判断即可.
解答 解:
在△ABC和△ADC中
∵AB=AD,AC=AC,
∴当CB=CD时,满足SSS,可证明△ABC≌△ACD,故A可以;
当∠BCA=∠DCA时,满足SSA,不能证明△ABC≌△ACD,故B不可以;
当∠BAC=∠DAC时,满足SAS,可证明△ABC≌△ACD,故C可以;
当∠B=∠D=90°时,满足HL,可证明△ABC≌△ACD,故D可以;
故选B.
点评 本题主要考查全等三角形的判定,掌握全等三角形的判定方法是解题关键,即SSS、SAS、ASA、AAS和HL.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
1.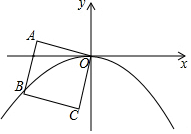 如图,正方形OABC的边长为2,OA与x轴负半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为( )
如图,正方形OABC的边长为2,OA与x轴负半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为( )
 如图,正方形OABC的边长为2,OA与x轴负半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为( )
如图,正方形OABC的边长为2,OA与x轴负半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为( )| A. | $-\frac{1}{2}$ | B. | $-\frac{{\sqrt{2}}}{6}$ | C. | -2 | D. | $-\frac{{\sqrt{2}}}{3}$ |
8.下列表述中,能确定准确位置的是( )
| A. | 教室第三排 | B. | 湖心南路 | ||
| C. | 南偏东40° | D. | 东经112°,北纬51° |
2.下列利用等式的性质,错误的是( )
| A. | 由a=b,得到1-a=1-b | B. | 由$\frac{a}{2}$=$\frac{b}{2}$,得到a=b | ||
| C. | 由a=b,得到ac=bc | D. | 由ac=bc,得到a=b |
 在△ABC中,已知点D,E,F分别是BC、AD、CE的中点,且三角形ABC的面积等于4cm2,则三角形BEF的面积等于1cm2.
在△ABC中,已知点D,E,F分别是BC、AD、CE的中点,且三角形ABC的面积等于4cm2,则三角形BEF的面积等于1cm2.