题目内容
3.已知:∠AOB=70°,∠AOC=30°,OD平分∠BOC,则∠AOD的度数为50°或20°.分析 利用角的和差关系计算.根据题意可得此题要分两种情况,一种是OC在∠AOB内部,另一种是OC∠AOB外部.
解答 解:分两种情况进行讨论: ①如图1,射线OC在∠AOB的内部.
①如图1,射线OC在∠AOB的内部.
∵∠BOC=∠AOB-∠BOC,∠AOB=70°,∠AOC=30°,
∴∠BOC=70°-30°=40°.
又∵0D平分∠BOC,
∴∠COD=20°,
∴∠AOD=∠COD+∠AOC=50°;
②如图2,射线OC在∠AOB的外部.
∵∠BOC=∠AOB+∠BOC,∠AOB=70°,∠AOC=30°,
∴∠BOC=70°+30°=100°.
又∵0D平分∠BOC,
∴∠COD=50°,
∴∠AOD=∠COD-∠AOC=20°.
综上所述,∠AOD=50°或20°.
故答案为:50°或20°.
点评 本题考查了角的计算,角平分线的定义.要根据射线OC的位置不同,分类讨论,分别求出∠AOD的度数.

练习册系列答案
相关题目
13.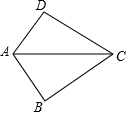 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )| A. | CB=CD | B. | ∠BCA=∠DCA | C. | ∠BAC=∠DAC | D. | ∠B=∠D=90° |
14.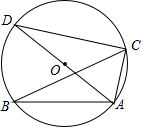 如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=25°,则∠CAD的度数是( )
如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=25°,则∠CAD的度数是( )
 如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=25°,则∠CAD的度数是( )
如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=25°,则∠CAD的度数是( )| A. | 25° | B. | 60° | C. | 65° | D. | 75° |
11.下列数中是无理数的是( )
| A. | $-\frac{11}{9}$ | B. | $\sqrt{\frac{1}{4}}$ | C. | $\sqrt{16}$ | D. | $\frac{π}{2}$ |
18. 下面四个图形中,经过折叠能围成如图所示的几何图形的是( )
下面四个图形中,经过折叠能围成如图所示的几何图形的是( )
 下面四个图形中,经过折叠能围成如图所示的几何图形的是( )
下面四个图形中,经过折叠能围成如图所示的几何图形的是( )| A. |  | B. |  | C. |  | D. |  |
15.下列运算正确的是( )
| A. | (-a)3÷(-a)=a2 | B. | (a2)3=a5 | C. | a2•a3=a6 | D. | a3+a2=a5 |