题目内容
1.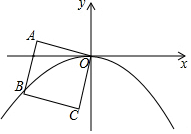 如图,正方形OABC的边长为2,OA与x轴负半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为( )
如图,正方形OABC的边长为2,OA与x轴负半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为( )| A. | $-\frac{1}{2}$ | B. | $-\frac{{\sqrt{2}}}{6}$ | C. | -2 | D. | $-\frac{{\sqrt{2}}}{3}$ |
分析 连接OB,过B作BD⊥x轴于D,若OA与x轴负半轴的夹角为15°,那么∠BOD=30°;在正方形OABC中,已知了边长,易求得对角线OB的长,进而可在Rt△OBD中求得BD、OD的值,也就得到了B点的坐标,然后将其代入抛物线的解析式中,即可求得待定系数a的值.
解答 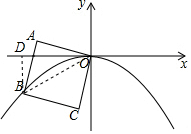 解:如图,连接OB,过B作BD⊥x轴于D;
解:如图,连接OB,过B作BD⊥x轴于D;
则∠BOA=45°,∠BOD=30°;
已知正方形的边长为2,则OB=2$\sqrt{2}$;
Rt△OBD中,OB=2$\sqrt{2}$,∠BOD=30°,则:
BD=$\frac{1}{2}$OB=$\sqrt{2}$,OD=$\sqrt{3}$OB=$\sqrt{6}$;
故B(-$\sqrt{6}$,-$\sqrt{2}$),
代入抛物线的解析式中,得:(-$\sqrt{6}$)2a=-$\sqrt{2}$,
解得a=-$\frac{\sqrt{2}}{6}$;
故选B.
点评 此题主要考查了正方形的性质、直角三角形的性质以及用待定系数法确定函数解析式的方法,能够正确地构造出与所求相关的直角三角形,是解决问题的关键.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
16.-2的倒数是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |
13.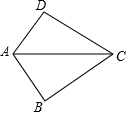 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )| A. | CB=CD | B. | ∠BCA=∠DCA | C. | ∠BAC=∠DAC | D. | ∠B=∠D=90° |
11.下列数中是无理数的是( )
| A. | $-\frac{11}{9}$ | B. | $\sqrt{\frac{1}{4}}$ | C. | $\sqrt{16}$ | D. | $\frac{π}{2}$ |
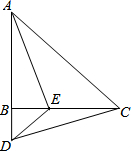 如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC上,且BE=BD,连结AE、DE、DC,试探索AE和DC的关系.
如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC上,且BE=BD,连结AE、DE、DC,试探索AE和DC的关系. 在方格纸中.选择一个空白的小正方形涂黑.使其与图中阴影部分构成轴对称图形,则符合要求的小正方形有3个.
在方格纸中.选择一个空白的小正方形涂黑.使其与图中阴影部分构成轴对称图形,则符合要求的小正方形有3个.