题目内容
已知二次函数y=ax2+bx+c的图象过点C(0,
),与x轴交于两点A(x1,0),B(x2,0)(x2<x1),且x1、x2是方程x2-4x-5=0的两实数根.
(1)求A、B两点的坐标;
(2)求二次函数的解析式及顶点坐标.
| 3 |
| 5 |
(1)求A、B两点的坐标;
(2)求二次函数的解析式及顶点坐标.
考点:抛物线与x轴的交点
专题:计算题
分析:(1)根据抛物线与x轴的交点问题解方程x2-4x-5=0即可得到A、B两点的坐标;
(2)利用交点式求解析式:设抛物线解析式为y=a(x-5)(x+1),再把点C坐标代入求出a即可得到抛物线解析式,然后利用抛物线的对称性得到对称轴为直线x=2,于是计算自变量为2的函数值即可得到抛物线的顶点坐标.
(2)利用交点式求解析式:设抛物线解析式为y=a(x-5)(x+1),再把点C坐标代入求出a即可得到抛物线解析式,然后利用抛物线的对称性得到对称轴为直线x=2,于是计算自变量为2的函数值即可得到抛物线的顶点坐标.
解答:解:(1)解方程x2-4x-5=0得x1=5,x2=-1,
所以A(5,0),B(-1,0);
(2)设抛物线解析式为y=a(x-5)(x+1),
把点C(0,
)代入得a•(-5)•1=
,解得a=-
,
所以抛物线解析式为y=-
(x-5)(x+1)=-
x2+
x+
,
当x=2时,y=-
(x-5)(x+1)=
,
所以抛物线的顶点坐标为(2,
).
所以A(5,0),B(-1,0);
(2)设抛物线解析式为y=a(x-5)(x+1),
把点C(0,
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 25 |
所以抛物线解析式为y=-
| 3 |
| 25 |
| 3 |
| 25 |
| 12 |
| 25 |
| 3 |
| 5 |
当x=2时,y=-
| 3 |
| 25 |
| 27 |
| 25 |
所以抛物线的顶点坐标为(2,
| 27 |
| 25 |
点评:本题考查了抛物线与x轴的交点:二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系,△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.利用抛物线的交点式求解析式简便.

练习册系列答案
相关题目
下列是计算正确的是( )
| A、-8-3=-5 |
| B、-(-2)2=4 |
| C、-(x-y)=x+y |
| D、ab+2ba=3ab |
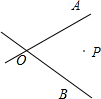 如图,两条公路OA、OB相交,在两条公路中间有一个油库,设为点P,如在两条公路上各设置一个加油站,请你设置一个方案,把两个加油站设在何处,可使油车从油库出发,经过一个加油站,再到另一个加油站,最后回到油库所走的路程最短.
如图,两条公路OA、OB相交,在两条公路中间有一个油库,设为点P,如在两条公路上各设置一个加油站,请你设置一个方案,把两个加油站设在何处,可使油车从油库出发,经过一个加油站,再到另一个加油站,最后回到油库所走的路程最短.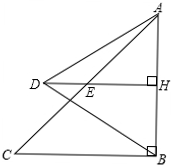 已知,如图:△ABC是等腰直角三角形,∠ABC=90°,D为△ABC外一点,连接AD、BD,过点D作DH⊥AB,垂足为H,交AC于E,已知AD=BD=2.
已知,如图:△ABC是等腰直角三角形,∠ABC=90°,D为△ABC外一点,连接AD、BD,过点D作DH⊥AB,垂足为H,交AC于E,已知AD=BD=2.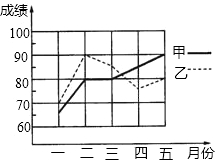 为了从甲、乙两名学生中选拔一人代表我校参加今年年底的全区中学生数学竞赛,统计了他们从今年1到5月的每个月的一次测验成绩(单位:分),如图是两人赛前5次测验成绩的折线统计图.
为了从甲、乙两名学生中选拔一人代表我校参加今年年底的全区中学生数学竞赛,统计了他们从今年1到5月的每个月的一次测验成绩(单位:分),如图是两人赛前5次测验成绩的折线统计图.