题目内容
在△ABC中,∠ACB=90°,∠B=30°,过点C作CD⊥AB于D.过点D作DE⊥BC于E,求证:BE=3CE.
考点:含30度角的直角三角形
专题:证明题
分析:求出∠CDB=∠DEC=90°,根据三角形内角和定理求出∠DCB=60°,根据三角形内角和定理∠CDE=30°,在Rt△DEC中和在Rt△DB中根据含30度角的直角三角形性质求出CD=2CE,BC=2CD,推出BC=4CE即可.
解答: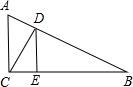 证明:∵CD⊥AB,DE⊥BC,
证明:∵CD⊥AB,DE⊥BC,
∴∠CDB=∠DEC=90°,
∵∠B=30°,
∴∠DCB=60°,
∴∠CDE=30°,
在Rt△DEC中,CD=2CE,
在Rt△DB中,BC=2CD,
∴BC=4CE,
∴BE=3CE.
 证明:∵CD⊥AB,DE⊥BC,
证明:∵CD⊥AB,DE⊥BC,∴∠CDB=∠DEC=90°,
∵∠B=30°,
∴∠DCB=60°,
∴∠CDE=30°,
在Rt△DEC中,CD=2CE,
在Rt△DB中,BC=2CD,
∴BC=4CE,
∴BE=3CE.
点评:本题考查了三角形的内角和定理和含30度角的直角三角形性质的应用,注意:在直角三角形中,如果有一个角等于30度,那么它所对的直角边等于斜边的一半.

练习册系列答案
相关题目
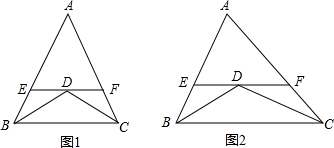
 如图,∠CAB=90°,AC=2,∠B=30°,作AC1⊥BC,再过点C1作C1A1⊥AB,…求图中所有阴影部分的面积.
如图,∠CAB=90°,AC=2,∠B=30°,作AC1⊥BC,再过点C1作C1A1⊥AB,…求图中所有阴影部分的面积. 如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O(A不与O重合),连接AO,如果AB=6,AO=4
如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O(A不与O重合),连接AO,如果AB=6,AO=4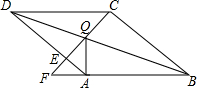 在菱形ABCD中,点Q是对角线DB上一点,连接CQ并延长,交AD于点E,交BA的延长线于点F,连接AQ.
在菱形ABCD中,点Q是对角线DB上一点,连接CQ并延长,交AD于点E,交BA的延长线于点F,连接AQ.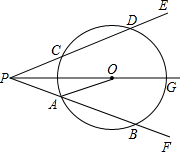 如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心、10为半径作⊙O,分别与∠EPF的两边相交于A,B和C,D,连接OA,此时有OA∥PE,若弦AB=12,求OP的长.
如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心、10为半径作⊙O,分别与∠EPF的两边相交于A,B和C,D,连接OA,此时有OA∥PE,若弦AB=12,求OP的长.