题目内容
如图1,将长方形纸片沿对角线AC折叠,使点D与点M重合,AM与DC交于点N,请判断△CAN的形状并说明理由.如图2,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在D′处,若AB=3,AD=4,AC=5,求AE的长.


考点:翻折变换(折叠问题)
专题:
分析:如图1,证明∠DAC=∠ACN;进而证明∠ACN=∠NAC,即可解决问题.
如图2,证明∠AD′E=90°;设AE=λ,则D′E=DE=4-λ,由勾股定理列出方程λ2=22+(4-λ)2,即可解决问题.
如图2,证明∠AD′E=90°;设AE=λ,则D′E=DE=4-λ,由勾股定理列出方程λ2=22+(4-λ)2,即可解决问题.
解答: 解:(1)如图1,
解:(1)如图1,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠DAC=∠ACN;
由题意得:∠DAC=∠NAC,
∴∠ACN=∠NAC,
∴AN=CN,△ANC为等腰三角形.
(2)∵四边形ABCD是矩形,
∴∠B=∠D=90°,DC=AB=3;
由题意得:∠AD′E=∠D=90°,D′C=DC=3,
∴AD′=5-3=2;设AE=λ,则D′E=DE=4-λ,
由勾股定理得:λ2=22+(4-λ)2,
解得:λ=2.5,
即AE的长=2.5.
 解:(1)如图1,
解:(1)如图1,∵四边形ABCD为矩形,
∴AD∥BC,
∴∠DAC=∠ACN;
由题意得:∠DAC=∠NAC,
∴∠ACN=∠NAC,
∴AN=CN,△ANC为等腰三角形.
(2)∵四边形ABCD是矩形,
∴∠B=∠D=90°,DC=AB=3;
由题意得:∠AD′E=∠D=90°,D′C=DC=3,
∴AD′=5-3=2;设AE=λ,则D′E=DE=4-λ,
由勾股定理得:λ2=22+(4-λ)2,
解得:λ=2.5,
即AE的长=2.5.
点评:该题主要考查了翻折变换的性质及其应用问题;解题的关键是灵活运用矩形的性质、等腰三角形的判定、勾股定理等几何知识点来分析、判断、推理或解答.

练习册系列答案
相关题目
 如图,四边形ABCD的四个顶点都在⊙O上,AC⊥BD于E,OF⊥AB于F,求证:2OF=CD.
如图,四边形ABCD的四个顶点都在⊙O上,AC⊥BD于E,OF⊥AB于F,求证:2OF=CD. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①c<0,②b>0,③4a+2b+c>0,④(a+c)2<b2,⑤b+2a=0;⑥△<0,其中正确的是
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①c<0,②b>0,③4a+2b+c>0,④(a+c)2<b2,⑤b+2a=0;⑥△<0,其中正确的是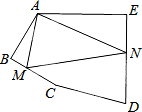 如图,在五边形ABCDE中,∠BAE=125°,∠B=∠E=90°,AB=BC,AE=DE,在BC、DE上分别找一点M、N,使得△AMN周长最小时,∠AMN+∠ANM的度数为
如图,在五边形ABCDE中,∠BAE=125°,∠B=∠E=90°,AB=BC,AE=DE,在BC、DE上分别找一点M、N,使得△AMN周长最小时,∠AMN+∠ANM的度数为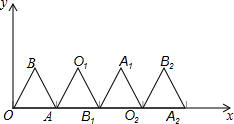 如图,在平面直角坐标系中有一个等边△OBA,其中A点坐标为(1,0).将△OBA绕顶点A顺时针旋转120°,得到△AO1B1;将得到的△AO1B1绕顶点B1顺时针旋转120°,得到△B1A1O2;然后再将得到的△B1A1O2绕顶点O2顺时针旋转120°,得到△O2B2A2…按照此规律,继续旋转下去,则A2014点的坐标为
如图,在平面直角坐标系中有一个等边△OBA,其中A点坐标为(1,0).将△OBA绕顶点A顺时针旋转120°,得到△AO1B1;将得到的△AO1B1绕顶点B1顺时针旋转120°,得到△B1A1O2;然后再将得到的△B1A1O2绕顶点O2顺时针旋转120°,得到△O2B2A2…按照此规律,继续旋转下去,则A2014点的坐标为 请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.