题目内容
已知：某等腰三角形的周长为36，腰长为x，底边长为y，则y与x之间的函数关系式是 ，定义域是 ．
考点：函数关系式,函数自变量的取值范围
专题：
分析：根据三角新的周长公式，可得函数解析式；根据等腰三角形三边的关系，可得x的取值范围．
解答：解：由三角形的周长公式，得y=36-2x，
由两边之和大于第三边，得
，
解36-2x+x＞x得x＜18，
解x+x＞36-2x得x＞9，
定义域是9＜x＜18，
故答案为：y=-2x+36，9＜x＜18．
由两边之和大于第三边，得
|
解36-2x+x＞x得x＜18，
解x+x＞36-2x得x＞9，
定义域是9＜x＜18，
故答案为：y=-2x+36，9＜x＜18．
点评：本题考查了函数关系式，利用三角形两边之和大于第三边得出不等式组是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
下列各式正确的是（ ）
| A、（a+1）-（-b+c）=a+1+b+c |
| B、a2-2（a-b+c）=a2-2a-b+c |
| C、a-2b+7c=a-（2b-7c） |
| D、a-b+c-d=（a-d）-（b+c） |
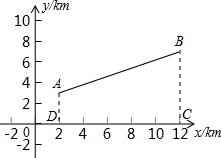去冬今春，济宁市遭遇了200年不遇的大旱，某乡镇为了解决抗旱问题，要在某河道建一座水泵站，分别向河的同一侧张村A和李村B送水．经实地勘查后，工程人员设计图纸时，以河道上的大桥O为坐标原点，以河道所在的直线为x轴建立直角坐标系（如图）．两村的坐标分别为A（2，3），B（12，7）．
如图所示，⊙O的半径为R，AB、CD是⊙O的任意两条弦，且AB垂直CD于M，求：AB2+（CM-DM）2．