题目内容
如图，四边形ABCD的四个顶点都在⊙O上，AC⊥BD于E，OF⊥AB于F，求证：2OF=CD．考点：圆周角定理,三角形中位线定理
专题：证明题
分析：如图，作辅助线；证明∠DBC=∠BAG，得到BG=DC；证明OF是△ABG的中位线，得到BG=2OF，即可解决问题．
解答：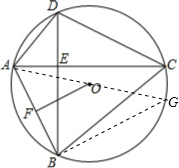
证明：如图，连接AO并延长，交⊙O于点G；
则∠ABG=90°；而AC⊥BD，
∴∠DBC=90°-∠ACB，∠BAG=90°-∠AGB，
∵∠ACB=∠AGB，
∴∠DBC=∠BAG，
∴BG=DC；
∵OF⊥AB，∠ABG=90°，
∴OF∥BG，AF=BF；而OA=OG，
∴OF是△ABG的中位线，
∴BG=2OF，
∴2OF=CD．
证明：如图，连接AO并延长，交⊙O于点G；则∠ABG=90°；而AC⊥BD，
∴∠DBC=90°-∠ACB，∠BAG=90°-∠AGB，
∵∠ACB=∠AGB，
∴∠DBC=∠BAG，
∴BG=DC；
∵OF⊥AB，∠ABG=90°，
∴OF∥BG，AF=BF；而OA=OG，
∴OF是△ABG的中位线，
∴BG=2OF，
∴2OF=CD．
点评：该题以圆为载体，以考查圆周角定理及其推论、三角形的中位线定理及其应用问题；解题的关键是作中位线，灵活运用有关定理来分析、解答．
练习册系列答案
相关题目
下列各式正确的是（ ）
| A、（a+1）-（-b+c）=a+1+b+c |
| B、a2-2（a-b+c）=a2-2a-b+c |
| C、a-2b+7c=a-（2b-7c） |
| D、a-b+c-d=（a-d）-（b+c） |
下列说法正确的是（ ）
| A、过A，B两点的直线长是A，B两点间的距离 |
| B、线段AB是A、B两点间的距离 |
| C、射线AB是A，B两点间的距离 |
| D、连接A，B两点的所有线中，线段AB的长度就是A，B两点间的距离 |
