题目内容
 请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
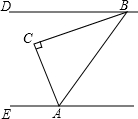
请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.A.如图,在△ABC中,∠C=90°.若BD∥AE,∠DBC=20°,则∠CAE的度数是
B.用科学计算器计算:
| 19 |
考点:计算器—三角函数,平行线的性质
专题:
分析:(1)过点C作CF∥BD,由平行线的性质可得CF∥AE,然后由两直线平行内错角相等,可得∠DBC+∠CAE=∠C,即可计算∠CAE的度数;
(2)正确使用计算器计算即可.
(2)正确使用计算器计算即可.
解答:解:(1)过点C作CF∥BD,如图所示:

∵BD∥AE,CF∥BD,
∴AE∥CF,
∴∠DBC=∠BCF,∠EAC=∠ACF,
∴∠DBC+∠EAC=∠BCF+∠ACF=∠C=90°,
∵∠DBC=20°,
∴∠EAC=∠CAE=∠C-∠DBC=90°-20°=70°.
故答案为:70°;
(2)
sin58°≈4.3589×0.8480≈3.70.
故答案为:3.70.

∵BD∥AE,CF∥BD,
∴AE∥CF,
∴∠DBC=∠BCF,∠EAC=∠ACF,
∴∠DBC+∠EAC=∠BCF+∠ACF=∠C=90°,
∵∠DBC=20°,
∴∠EAC=∠CAE=∠C-∠DBC=90°-20°=70°.
故答案为:70°;
(2)
| 19 |
故答案为:3.70.
点评:此题考查了(1)平行线的性质(2)利用计算器计算三角函数的有关知识,解题的关键是:(1)正确添加辅助线,(2)正确使用计算器.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
-3的相反数是( )
| A、3 | ||
B、
| ||
| C、-3 | ||
D、-
|
计算(x2-4)÷(x-2)=( )
| A、x-2 |
| B、x+2 |
| C、2-x |
| D、x2-4 |

 如图,点A、O、B在一条直线上,∠AOC=140°,OD是∠BOC的平分线,则∠COD=
如图,点A、O、B在一条直线上,∠AOC=140°,OD是∠BOC的平分线,则∠COD=