题目内容
5.直线x-y=1与反比例函数$y=\frac{k}{x}$的图象如果恰有一个交点,则该交点必定在第四象限.分析 由直线的解析式可知直线经过一三四象限,若反比例函数的图象在一三象限必定有两个交点,所以只有在二四象限才有可能有一个交点,据此即可判断.
解答 解:由x-y=1化成y=x-1可知直线经过一三四象限,
∵直线x-y=1与反比例函数$y=\frac{k}{x}$的图象如果恰有一个交点,
∴反比例函数$y=\frac{k}{x}$的图象应该在二四象限,
∴该交点必定在第四象限,
故答案为:四.
点评 本题考查了反比例函数和一次函数的交点问题,熟练掌握反比例函数和一次函数的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.三张外形完全相同的卡片上分别画有等腰直角三角形、菱形、圆,把它们从中间剪开变成了6张小卡片,把这6张小卡片放到一个不透明的盒子中,摇匀后随机抽取两张小卡片,则这两张小卡片上的图形恰好能拼成圆的概率是( )
| A. | $\frac{1}{30}$ | B. | $\frac{1}{15}$ | C. | $\frac{1}{18}$ | D. | $\frac{1}{6}$ |
10. 如图,三角形ABC中,AB=AC,D,E分别为边AB,AC上的点,DM平分∠BDE,EN平分∠DEC,若∠DMN=110°,则∠DEA=( )
如图,三角形ABC中,AB=AC,D,E分别为边AB,AC上的点,DM平分∠BDE,EN平分∠DEC,若∠DMN=110°,则∠DEA=( )
 如图,三角形ABC中,AB=AC,D,E分别为边AB,AC上的点,DM平分∠BDE,EN平分∠DEC,若∠DMN=110°,则∠DEA=( )
如图,三角形ABC中,AB=AC,D,E分别为边AB,AC上的点,DM平分∠BDE,EN平分∠DEC,若∠DMN=110°,则∠DEA=( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
14.已知函数y=(m-1)xm2+m-2是x的一次函数,则常数m的值为( )
| A. | -1 | B. | 1或-1 | C. | 1 | D. | 2或-1 |
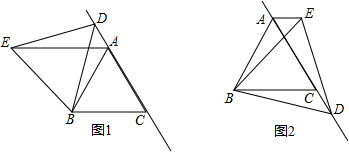
 如图,△ABD、△AEC都是等边三角形,直线CD与直线BE交于点F.
如图,△ABD、△AEC都是等边三角形,直线CD与直线BE交于点F. 一个几何体的正视图与左视图相同,均为如图所示,则其俯视图可能是( )
一个几何体的正视图与左视图相同,均为如图所示,则其俯视图可能是( )



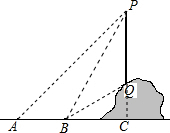 如图所示,从地面上一点A测出山顶电视塔的上端P点的仰角是45°,向前走60米到B点测得P点的仰角是60°,电视塔底部Q的仰角是30°,求电视塔PQ的高度(精确到1米)
如图所示,从地面上一点A测出山顶电视塔的上端P点的仰角是45°,向前走60米到B点测得P点的仰角是60°,电视塔底部Q的仰角是30°,求电视塔PQ的高度(精确到1米)