题目内容
4.下列各式书写规范的是( )| A. | ab2 | B. | s÷v | C. | 3$\frac{1}{2}$x | D. | -x |
分析 利用代数式书写格式要求判断即可.
解答 解:A、原式=2ab,不符合题意;
B、原式=$\frac{s}{v}$,不符合题意;
C、原式=$\frac{7}{2}$x,不符合题意;
D、原式符合题意,
故选D
点评 此题考查了代数式,熟练掌握代数式书写要求是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.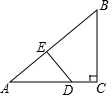 如图,在△ABC中,∠C=90°,点D、E分别在边AC、AB上.若∠B=∠ADE,则下列结论不正确的是( )
如图,在△ABC中,∠C=90°,点D、E分别在边AC、AB上.若∠B=∠ADE,则下列结论不正确的是( )
 如图,在△ABC中,∠C=90°,点D、E分别在边AC、AB上.若∠B=∠ADE,则下列结论不正确的是( )
如图,在△ABC中,∠C=90°,点D、E分别在边AC、AB上.若∠B=∠ADE,则下列结论不正确的是( )| A. | ∠A和∠B互为余角 | B. | ∠A和∠ADE互为余角 | ||
| C. | ∠B和∠EDC互为补角 | D. | ∠B和∠DEB互为补角 |
14.发现思考:已知等腰三角形ABC的两边分别是方程x2-7x+10=0的两个根,求等腰三角形ABC三条边的长各是多少?下边是涵涵同学的作业,老师说他的做法有错误,请你找出错误之处并说明错误原因.
涵涵的作业
探究应用:请解答以下问题:
已知等腰三角形ABC的两边是关于x的方程x2-mx+$\frac{m}{2}$-$\frac{1}{4}$=0的两个实数根.
(1)当m=2时,求△ABC的周长;
(2)当△ABC为等边三角形时,求m的值.
涵涵的作业
| 解:x2-7x+10=0 a=1 b=-7 c=10 ∵b2-4ac=9>0 ∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{7+3}{2}$ ∴x1=5,x2=2 所以,当腰为5,底为2时,等腰三角形的三条边为5,5,2. 当腰为2,底为5时,等腰三角形的三条边为2,2,5. |
已知等腰三角形ABC的两边是关于x的方程x2-mx+$\frac{m}{2}$-$\frac{1}{4}$=0的两个实数根.
(1)当m=2时,求△ABC的周长;
(2)当△ABC为等边三角形时,求m的值.
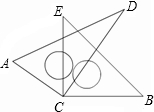 如图,将两块直角三角尺的直角顶点C叠放在一起.
如图,将两块直角三角尺的直角顶点C叠放在一起.