题目内容
2．若3a=2，3b=6，3c=12，a，b，c的关系不正确的是（ ）| A． | b=a+1 | B． | c=a+b+1 | C． | 2b=c+1 | D． | c=2a+1 |
分析 根据同底数幂的乘法法则求解．
解答 解：∵3a•3b=2×6=12=3c，
∴a+b=c，故B错误；
∵3a•3=2×3=6=3b，
∴a+1=b，故A正确；
∵（3b）2=36=3c•3=36，
∴2b=c+1，故C正确；
∵32a+1=12=3c，
∴2a+1=c，故D正确．
故选B．
点评 本题考查了同底数幂的乘法，解答本题的关键是掌握同底数幂的乘法法则．
练习册系列答案
相关题目
12．下列各式能用平方差公式计算的是（ ）
| A． | （2a+b）（2b-a） | B． | （-a+b）（a-b） | C． | （a+b）（a-2b） | D． | （a+b）（b-a） |
如图，∠1=∠2，∠3+∠4=180°，试问：直线a与直线c是否平行？并说明理由．
20．意大利著名数学家芬波那在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…，其中从第三个数值起，每一个数都等于它前面两个数的和，现以这组数中的各个数作为正方形的边长值构造如下正方形：
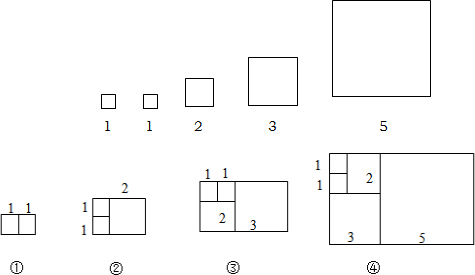
两分别依次从左到右取2个、3个、4个、5个…正方形拼成如下长方形并记为①、②、③、④、…相应长方形的周长如表所示：
（1）仔细观察图形，表中的x=16，y=26；
（2）若按此规律继续拼成长方形，则序号为④的长方形周长是26（并写出简要的过程）
（3）以下①、②小题只需选做一小题，若两小题都写，则只按第①小题的解答给分．
①若按此规律拼长方形，已知序号为n的长方形的周长为a，序号为（n+1）的长方形的周长为b，则序号为（n+3）的长方形的周长为a+2b（用含a、b的代数式表示）
②若按此规律继续拼长方形，已知序号为n的长方形的长和宽分别为a、b（其中a＜b），则序号为（n+1）的长方形的周长是2a+4b（用含a、b的代数式表示）．
两分别依次从左到右取2个、3个、4个、5个…正方形拼成如下长方形并记为①、②、③、④、…相应长方形的周长如表所示：
| 序号 | ① | ② | ③ | ④ | … |
| 周长 | 6 | 10 | x | y | … |
（2）若按此规律继续拼成长方形，则序号为④的长方形周长是26（并写出简要的过程）
（3）以下①、②小题只需选做一小题，若两小题都写，则只按第①小题的解答给分．
①若按此规律拼长方形，已知序号为n的长方形的周长为a，序号为（n+1）的长方形的周长为b，则序号为（n+3）的长方形的周长为a+2b（用含a、b的代数式表示）
②若按此规律继续拼长方形，已知序号为n的长方形的长和宽分别为a、b（其中a＜b），则序号为（n+1）的长方形的周长是2a+4b（用含a、b的代数式表示）．