题目内容
3．一个正多边形的内角和为1080°，则这个正多边形的每个外角为（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 80° |
分析 根据多边形的内角和公式（n-2）•180°列式进行计算求得边数，然后根据多边形的外角和即可得到结论．
解答 解：设它是n边形，则
（n-2）•180°=1080°，
解得n=8．
360°÷8=45°，
故选B．
点评 本题考查了多边形的内角和公式，熟记公式是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
13．若A（-1，y1），B（-5，y2），C（0，y3）为二次函数y=x2+4x-5的图象上的三点，则y1，y2，y3的大小关系是（ ）
| A． | y1＜y2＜y3 | B． | y2＜y1＜y3 | C． | y3＜y1＜y2 | D． | y1＜y3＜y2 |
14．下列实数中，无理数是（ ）
| A． | 2 | B． | 3.333 | C． | -π | D． | $\sqrt{4}$ |
11．下列计算正确的是（ ）
| A． | （-2a2）3=8a6 | B． | （-$\frac{1}{2}$）-1=$\frac{1}{2}$ | C． | $\sqrt{9}$=±3 | D． | a10÷a5=a5 |
18．
如图，AB是⊙O的直径，弦CD⊥AB，∠CAB=40°，连接BD、OD，则∠AOD+∠ABD的度数为（ ）
如图，AB是⊙O的直径，弦CD⊥AB，∠CAB=40°，连接BD、OD，则∠AOD+∠ABD的度数为（ ）| A． | 100° | B． | 110° | C． | 120° | D． | 150° |
如图，Rt△ABC中，∠C=90°，BC=15，tanA=$\frac{15}{8}$，则AB=17．
15．从标有号数1到10的10张卡片中，随意抽取一张，其号数为3的倍数的概率是（ ）
| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{3}{10}$ | D． | 无法确定 |
12．计算（-1+2）×（-$\frac{1}{2}$）2÷（-2）的结果是（ ）
| A． | 8 | B． | -8 | C． | $\frac{1}{8}$ | D． | $-\frac{1}{8}$ |
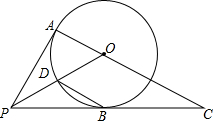如图，PA，PB是⊙O的切线，A，B为切点，连接AO并延长，交PB的延长线于点C，连接PO，交⊙O于点D．