题目内容
13.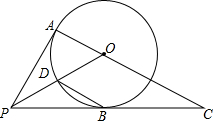 如图,PA,PB是⊙O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.
如图,PA,PB是⊙O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.(1)求证:PO平分∠APC;
(2)连接DB,若∠C=30°,求证:DB∥AC.
分析 (1)连接OB,根据角平分线性质定理的逆定理,即可解答;
(2)先证明△ODB是等边三角形,得到∠OBD=60°,再由∠DBP=∠C,即可得到DB∥AC.
解答 解:(1)如图,连接OB,
∵PA,PB是⊙O的切线,
∴OA⊥AP,OB⊥BP,
又OA=OB,
∴PO平分∠APC;
(2)∵OA⊥AP,OB⊥BP,
∴∠CAP=∠OBP=90°,
∵∠C=30°,
∴∠APC=90°-∠C=90°-30°=60°,
∵PO平分∠APC,
∴∠OPC=$\frac{1}{2}$∠APC=$\frac{1}{2}×60°$=30°,
∴∠POB=90°-∠OPC=90°-30°=60°,
又OD=OB,
∴△ODB是等边三角形,
∴∠OBD=60°,
∴∠DBP=∠OBP-∠OBD=90°-60°=30°,
∴∠DBP=∠C,
∴DB∥AC.
点评 本题考查了切线的性质,角平分线的判定,等边三角形的判定和性质,解本题的关键是判断出△ODB是等边三角形.

练习册系列答案
相关题目
3.一个正多边形的内角和为1080°,则这个正多边形的每个外角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 80° |
4. 如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )
如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )
 如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )
如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )| A. | x-y2=3 | B. | 2x-y2=9 | C. | 3x-y2=15 | D. | 4x-y2=21 |
8.下列运算中,正确的是( )
| A. | 7a+a=7a2 | B. | a2•a3=a6 | C. | a3÷a=a2 | D. | (ab)2=ab2 |
5.若a-b=2,b-c=-3,则a-c等于( )
| A. | 1 | B. | -1 | C. | 5 | D. | -5 |
2.(-21)÷7的结果是( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | $-\frac{1}{3}$ |
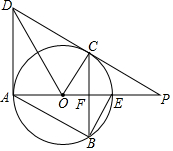 如图所示,直线DP和圆O相切于点C,交直径AE的延长线于点P.过点C作AE的垂线,交AE于点F,交圆O于点B.作平行四边形ABCD,连接BE,DO,CO.
如图所示,直线DP和圆O相切于点C,交直径AE的延长线于点P.过点C作AE的垂线,交AE于点F,交圆O于点B.作平行四边形ABCD,连接BE,DO,CO.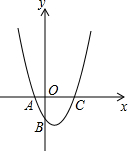 如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧,其图象与x轴交于点A(-1,0)与点C(x2,0),且与y轴交于点B(0,-2),小强得到以下结论:①0<a<2;②-1<b<0;③c=-1;④当|a|=|b|时x2>$\sqrt{5}$-1;以上结论中正确结论的序号为①④.
如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧,其图象与x轴交于点A(-1,0)与点C(x2,0),且与y轴交于点B(0,-2),小强得到以下结论:①0<a<2;②-1<b<0;③c=-1;④当|a|=|b|时x2>$\sqrt{5}$-1;以上结论中正确结论的序号为①④.