题目内容
8. 如图,Rt△ABC中,∠C=90°,BC=15,tanA=$\frac{15}{8}$,则AB=17.
如图,Rt△ABC中,∠C=90°,BC=15,tanA=$\frac{15}{8}$,则AB=17.
分析 根据∠A的正切求出AC,再利用勾股定理列式计算即可得解.
解答 解:∵Rt△ABC中,∠C=90°,tanA=$\frac{15}{8}$,BC=15,
∴$\frac{15}{AC}$=$\frac{15}{8}$,
解得AC=8,
根据勾股定理得,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{8}^{2}+1{5}^{2}}$=17.
故答案为:17.
点评 本题考查了解直角三角形,勾股定理,主要利用了锐角的正切等于对边比邻边.

练习册系列答案
相关题目
18.2017的倒数是( )
| A. | -2017 | B. | 2017 | C. | -$\frac{1}{2017}$ | D. | $\frac{1}{2017}$ |
19.在2017年十堰市初中体育中考中,随意抽取某校5位同学跳远的记录分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
| A. | 平均数为160 | B. | 中位数为158 | C. | 众数为158 | D. | 方差为20.3 |
16. 如图,直线a∥b,若∠1=40°,∠2=55°,则∠3的度数为( )
如图,直线a∥b,若∠1=40°,∠2=55°,则∠3的度数为( )
 如图,直线a∥b,若∠1=40°,∠2=55°,则∠3的度数为( )
如图,直线a∥b,若∠1=40°,∠2=55°,则∠3的度数为( )| A. | 115° | B. | 105° | C. | 95° | D. | 85° |
3.一个正多边形的内角和为1080°,则这个正多边形的每个外角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 80° |
13.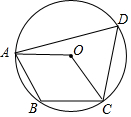 如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠DAO+∠DCO的大小为( )
如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠DAO+∠DCO的大小为( )
 如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠DAO+∠DCO的大小为( )
如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠DAO+∠DCO的大小为( )| A. | 45° | B. | 50° | C. | 60° | D. | 75° |
20.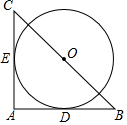 如图,在Rt△ABC中,∠A=90°,BC=2$\sqrt{2}$,以BC的中点O为圆心分别与AB,AC相切于D,E两点,则$\widehat{DE}$的长为( )
如图,在Rt△ABC中,∠A=90°,BC=2$\sqrt{2}$,以BC的中点O为圆心分别与AB,AC相切于D,E两点,则$\widehat{DE}$的长为( )
 如图,在Rt△ABC中,∠A=90°,BC=2$\sqrt{2}$,以BC的中点O为圆心分别与AB,AC相切于D,E两点,则$\widehat{DE}$的长为( )
如图,在Rt△ABC中,∠A=90°,BC=2$\sqrt{2}$,以BC的中点O为圆心分别与AB,AC相切于D,E两点,则$\widehat{DE}$的长为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
17.爱心图书馆决定给9个贫困山区捐赠图书,管理员小张对各个地区捐赠情况作了统计,并汇成了如下图表,下列结论不正确的是( )
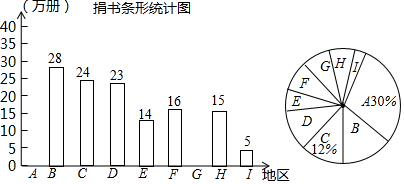
| 地区 | A | B | C | D | E | F | G | H | I |
| 万册 | 28 | 24 | 23 | 14 | 16 | 15 | 5 |

| A. | 捐书的总数为200万册 | |
| B. | 捐书数据的中位数是16万册 | |
| C. | 捐书数据的众数是60万册 | |
| D. | 捐书数扇形统计图中表示G的扇形的圆心角为30° |
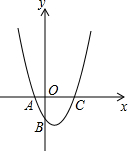 如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧,其图象与x轴交于点A(-1,0)与点C(x2,0),且与y轴交于点B(0,-2),小强得到以下结论:①0<a<2;②-1<b<0;③c=-1;④当|a|=|b|时x2>$\sqrt{5}$-1;以上结论中正确结论的序号为①④.
如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧,其图象与x轴交于点A(-1,0)与点C(x2,0),且与y轴交于点B(0,-2),小强得到以下结论:①0<a<2;②-1<b<0;③c=-1;④当|a|=|b|时x2>$\sqrt{5}$-1;以上结论中正确结论的序号为①④.