题目内容
15．从标有号数1到10的10张卡片中，随意抽取一张，其号数为3的倍数的概率是（ ）| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{3}{10}$ | D． | 无法确定 |
分析 让3的倍数的个数除以数的总数即为所求的概率．
解答 解：∵1到10的数字中是3的倍数的有3，6，9共3个，
∴卡片上的号数为3的倍数的概率是$\frac{3}{10}$．
故选C．
点评 本题考查概率的求法．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
口算能手系列答案
相关题目
5．下列计算，正确的是（ ）
| A． | a2•a3=a6 | B． | 3a2-a2=2 | C． | a8÷a2=a4 | D． | （-2a）3=-8a3 |
6．H7N9禽流感病毒的直径大约为0.0000000805米，这个数用科学记数法表示为（ ）
| A． | 8.05×10-8 | B． | 8.05×10-7 | C． | 80.5×10-9 | D． | 0.805×10-7 |
3．一个正多边形的内角和为1080°，则这个正多边形的每个外角为（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 80° |
10．二次根式$\sqrt{x+2}$中x的取值范围是（ ）
| A． | x≥-2 | B． | x≥2 | C． | x≥0 | D． | x＞-2 |
20．
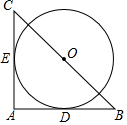如图，在Rt△ABC中，∠A=90°，BC=2$\sqrt{2}$，以BC的中点O为圆心分别与AB，AC相切于D，E两点，则$\widehat{DE}$的长为（ ）
如图，在Rt△ABC中，∠A=90°，BC=2$\sqrt{2}$，以BC的中点O为圆心分别与AB，AC相切于D，E两点，则$\widehat{DE}$的长为（ ）| A． | $\frac{π}{4}$ | B． | $\frac{π}{2}$ | C． | π | D． | 2π |
4．
如图，在△ABC中，AB=AC，BC=12，E为AC边的中点，线段BE的垂直平分线交边BC于点D．设BD=x，tan∠ACB=y，则（ ）
如图，在△ABC中，AB=AC，BC=12，E为AC边的中点，线段BE的垂直平分线交边BC于点D．设BD=x，tan∠ACB=y，则（ ）| A． | x-y2=3 | B． | 2x-y2=9 | C． | 3x-y2=15 | D． | 4x-y2=21 |
5．若a-b=2，b-c=-3，则a-c等于（ ）
| A． | 1 | B． | -1 | C． | 5 | D． | -5 |