题目内容
在△ABC中,DE∥BC,AB=6,AC=4,BC=5,且S△ADE=S四边形DBCE,则DE= .
考点:相似三角形的判定与性质
专题:
分析:由S△ADE=S四边形DBCE可知
=
,可求得其相似比为
=
,代入可求得DE.
| S△ADE |
| S△ABC |
| 1 |
| 2 |
| DE |
| BC |
| 1 | ||
|
解答:解:
∵DE∥BC,
∴△ADE∽△ABC,
∵S△ADE=S四边形DBCE,
∴
=
,
∴
=
,
即
=
,
解得DE=
,
故答案为:
.
∵DE∥BC,
∴△ADE∽△ABC,
∵S△ADE=S四边形DBCE,
∴
| S△ADE |
| S△ABC |
| 1 |
| 2 |
∴
| DE |
| BC |
| 1 | ||
|
即
| DE |
| 5 |
| 1 | ||
|
解得DE=
5
| ||
| 2 |
故答案为:
5
| ||
| 2 |
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的面积比等于相似比的平方,求出相似比是解题的关键.

练习册系列答案
相关题目
甲乙两人同时同地同向出发沿400米环形跑道跑步,甲的速度比乙快,当甲第二次追上乙时,甲比乙跑的路程( )
| A、一样多 | B、多800m |
| C、多400m | D、少400m |
 如图,已知∠1=∠2,若添一个条件就能使△ADE∽△ABC成立,则条件不能是( )
如图,已知∠1=∠2,若添一个条件就能使△ADE∽△ABC成立,则条件不能是( )| A、AD:AB=DE:BC |
| B、∠AED=∠C |
| C、∠D=∠B |
| D、AD:AB=AE:AC |
数-8不属于下列集合中的( )
| A、整数集合 | B、负数集合 |
| C、有理数集合 | D、非负数集合 |
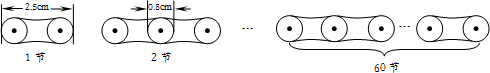

 如图,在Rt△ABC中,∠A=90°,AB=4,AC=2,点E为AC的中点,点F在边BC上,且FE⊥BE,则CF=
如图,在Rt△ABC中,∠A=90°,AB=4,AC=2,点E为AC的中点,点F在边BC上,且FE⊥BE,则CF=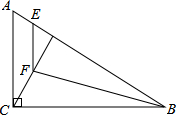 如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,点E在边AB上,且BE=BC,过点E作EF∥AC,交CD于F点,连接BF.
如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,点E在边AB上,且BE=BC,过点E作EF∥AC,交CD于F点,连接BF.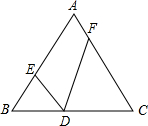 如图,在等边△ABC中,边长为6,D是BC边上的动点,∠EDF=60°.
如图,在等边△ABC中,边长为6,D是BC边上的动点,∠EDF=60°.