题目内容
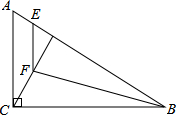 如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,点E在边AB上,且BE=BC,过点E作EF∥AC,交CD于F点,连接BF.
如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,点E在边AB上,且BE=BC,过点E作EF∥AC,交CD于F点,连接BF.(1)若BC=10,BD=8,求线段EF的长;
(2)求证:BF是∠ABC的平分线.
考点:相似三角形的判定与性质,角平分线的性质
专题:
分析:(1)由条件可得∠DFE=∠DBC,且∠EDF=∠CDB,可证得△DEF∽△DCB,利用对应边的比相等可求得EF;
(2)连接CE,利用等腰三角形的性质和平行的性质可得到∠FEC=∠FCE,可证得EF=CF,结合BE=BC,可知BF为CE的垂直平分线,结合等腰三角形的“三线合一”的性质可得到结论.
(2)连接CE,利用等腰三角形的性质和平行的性质可得到∠FEC=∠FCE,可证得EF=CF,结合BE=BC,可知BF为CE的垂直平分线,结合等腰三角形的“三线合一”的性质可得到结论.
解答:(1)解:
∵CD⊥AB,
∴∠EDF=∠CDB,
∵EF∥AC,
∴∠EFD=∠A,
∵∠ACB=90°,
∴∠A+∠DBC=∠DEF+∠DFE=90°,
∴∠DFE=∠DBC,
∴△DEF∽△DCB,
∴
=
,
∵BC=BE=10,BD=8,
∴CD=6,DE=BE-BD=2,
∴
=
,
解得EF=
;
(2)证明:
如图,连结EC,
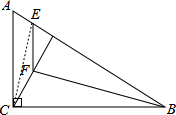
∵∠ACB=∠CDB=90°,
∴∠A=∠DCB,
∵EF∥AC,
∴∠A=∠FEB,
∴∠FEB=∠FCB,
∵BE=BC,
∴∠BEC=∠BCE,
∴∠FEC=∠FCE,
∴EF=CF,
∴BF⊥EC,
又BE=BC,
∴BF平分∠ABC.
∵CD⊥AB,
∴∠EDF=∠CDB,
∵EF∥AC,
∴∠EFD=∠A,
∵∠ACB=90°,
∴∠A+∠DBC=∠DEF+∠DFE=90°,
∴∠DFE=∠DBC,
∴△DEF∽△DCB,
∴
| EF |
| BC |
| DE |
| DC |
∵BC=BE=10,BD=8,
∴CD=6,DE=BE-BD=2,
∴
| EF |
| 10 |
| 2 |
| 6 |
解得EF=
| 10 |
| 3 |
(2)证明:
如图,连结EC,

∵∠ACB=∠CDB=90°,
∴∠A=∠DCB,
∵EF∥AC,
∴∠A=∠FEB,
∴∠FEB=∠FCB,
∵BE=BC,
∴∠BEC=∠BCE,
∴∠FEC=∠FCE,
∴EF=CF,
∴BF⊥EC,
又BE=BC,
∴BF平分∠ABC.
点评:本题主要考查相似三角形的判定和性质及全等三角形的判定和性质,利用相似求得EF的长是解题的关键,注意角平分线的判定方法可以证明角相等也可以证明点到角两边的距离相等.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
若抛物线y=ax2经过点P(1,-3),则此抛物线也经过点( )
| A、P(-1,3) |
| B、P(-3,1) |
| C、P (1,3) |
| D、P(-1,-3) |
 如图,在△ABC中,∠BAC=90°,AB=AC,若MN是经过点A的直线,BD⊥MN于D,CE⊥MN于E,求证:DE=BD+CE.
如图,在△ABC中,∠BAC=90°,AB=AC,若MN是经过点A的直线,BD⊥MN于D,CE⊥MN于E,求证:DE=BD+CE.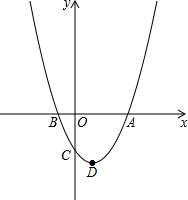 如图,已知抛物线y=ax2-2ax-b(a>0)与x轴的一个交点为B(-1,0),与y轴的负半轴交于点C,顶点为D.
如图,已知抛物线y=ax2-2ax-b(a>0)与x轴的一个交点为B(-1,0),与y轴的负半轴交于点C,顶点为D. 如图,已知:在△ABC中,点D、E分别在AB、AC上,S△ADE:S△BDE:S△BEC=4:2:3,求证:DE∥BC.
如图,已知:在△ABC中,点D、E分别在AB、AC上,S△ADE:S△BDE:S△BEC=4:2:3,求证:DE∥BC. 如图,△ABC中,BE平分∠ABC,CE平分∠ACB,DF经过点E,与AB,AC相交于点D,F,且DF∥BC.
如图,△ABC中,BE平分∠ABC,CE平分∠ACB,DF经过点E,与AB,AC相交于点D,F,且DF∥BC.