题目内容
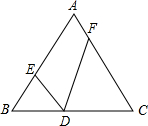 如图,在等边△ABC中,边长为6,D是BC边上的动点,∠EDF=60°.
如图,在等边△ABC中,边长为6,D是BC边上的动点,∠EDF=60°.(1)求证:△BDE∽△CFD;
(2)当BD=1,CF=3时,求BE的长.
考点:相似三角形的判定与性质,等边三角形的性质
专题:
分析:(1)由条件可得出∠BED+∠EDB=∠EDB+∠FDC=120°,可得到∠BED=∠FDC,且∠B=∠C,可证得结论;
(2)利用(1)结论可得出
=
,且CD=BC-BD=5,代入可求得BE.
(2)利用(1)结论可得出
| BE |
| CD |
| BD |
| CF |
解答:(1)证明:∵△ABC为等边三角形,
∴∠B=∠C=60°,
∵∠EDF=60°,
∴∠BED+∠EDB=∠EDB+∠FDC=120°,
∴∠BED=∠FDC,
∴△BDE∽△CFD;
(2)解:由(1)知△BDE∽△CFD,
∴
=
,
∵BC=6,BD=1,
∴CD=BC-BD=5,
∴
=
,
解得BE=
.
∴∠B=∠C=60°,
∵∠EDF=60°,
∴∠BED+∠EDB=∠EDB+∠FDC=120°,
∴∠BED=∠FDC,
∴△BDE∽△CFD;
(2)解:由(1)知△BDE∽△CFD,
∴
| BE |
| CD |
| BD |
| CF |
∵BC=6,BD=1,
∴CD=BC-BD=5,
∴
| BE |
| 5 |
| 1 |
| 3 |
解得BE=
| 5 |
| 3 |
点评:本题主要考查相似三角形的判定和性质,利用条件得到∠BED=∠FDC是解题的关键,注意等边三角形性质的应用.

练习册系列答案
相关题目
下列四个结论中,正确的是( )
A、
| ||||||||
B、
| ||||||||
C、1<
| ||||||||
D、
|
 如图,△ABC中,BE平分∠ABC,CE平分∠ACB,DF经过点E,与AB,AC相交于点D,F,且DF∥BC.
如图,△ABC中,BE平分∠ABC,CE平分∠ACB,DF经过点E,与AB,AC相交于点D,F,且DF∥BC.