题目内容
20.已知二次函数y=ax2+bx+c的图象与x轴交于(2,0),(x1,0)且1<x1<2,与y轴正半轴交点在(0,2)的下方,下列结论:①a<b<0;②b2-4ac>-8a;③4a+c<0;④2a-b+1<0,其中正确的是:②.分析 根据已知画出图象,得到抛物线开口向上,则a>0,由对称轴x=-$\frac{b}{2a}$>0可知b<0,由与y轴正半轴交点在(0,2)的下方可知0<c<2,由与x轴交于两点可知>0,根据结论判断即可.
解答  解:根据二次函数y=ax2+bx+c的图象与x轴交于点(2,0)、(x1,0),且1<x1<2,与y轴的正半轴的交点在(0,2)的下方,画出图象为:如图
解:根据二次函数y=ax2+bx+c的图象与x轴交于点(2,0)、(x1,0),且1<x1<2,与y轴的正半轴的交点在(0,2)的下方,画出图象为:如图
由图象开口向下知a>0,
由y=ax2+bx+c与x轴的另一个交点坐标为(x1,0 ),且1<x1<2,
则该抛物线的对称轴为x=-$\frac{b}{2a}$>0,
∴b<0,∴①错误;
∵抛物线与x轴有两个交点,
∴b2-4ac>0,
∵a>0,
∴-8a<0,
∴b2-4ac>-8a,∴②正确;
∵a>0,c>0,
∴4a+c>0,∴③错误;
∵a>0,b<0,
∴2a-b+1>0,∴④错误.
故答案为②.
点评 本题考查了二次函数和系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为一条抛物线,当a>0,抛物线的开口向上,在对称轴x=-$\frac{b}{2a}$的左侧,y随x的增大而减小,在对称轴x=-$\frac{b}{2a}$的右侧,y随x的增大而增大;当a<0,抛物线的开口向下,当x=-$\frac{b}{2a}$时,函数值最大;抛物线与y轴的交点坐标为(0,c).

练习册系列答案
相关题目
11.某自行车厂一局计划生产1400辆自行车,平均每天生产200辆,由于各种原因,实际上每天的生产量与计划量相比有出入,如表是某周的生产情况(实际上每天的生产量比计划量增产记为正,实际上每天的生产量比计划量减产记为负):
(1)根据记录可知,将这一周的每天生产填入表
(2)该厂实行计件工资制,若能完成每天计划的生产量,每生产一辆得60元,增产部分按每辆80元计算,如果不能完成每天计划的生产量,则每天生产一辆得50元,那么该厂工人这一周的工资总额是多少?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | -10 | +8 | -4 | +10 | +2 | +6 | -6 |
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 每天生产量(辆) | 190 | 208 | 196 | 210 | 202 | 206 | 194 |
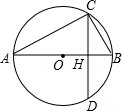 如图,AB为⊙O直径,弦CD⊥AB,垂足为H,已知⊙O的半径为2,CD=2$\sqrt{3}$.
如图,AB为⊙O直径,弦CD⊥AB,垂足为H,已知⊙O的半径为2,CD=2$\sqrt{3}$. 已知在纸面上有一数轴(如图),折叠纸面.
已知在纸面上有一数轴(如图),折叠纸面.