题目内容
15.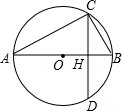 如图,AB为⊙O直径,弦CD⊥AB,垂足为H,已知⊙O的半径为2,CD=2$\sqrt{3}$.
如图,AB为⊙O直径,弦CD⊥AB,垂足为H,已知⊙O的半径为2,CD=2$\sqrt{3}$.(1)求弦AC的长;
(2)此圆周上到直线AC的距离为1的点有几个?说明你的理由.
分析 (1)作OF⊥AC于F,连接OC,则AF=CF,由垂径定理得出CH=DH=$\frac{1}{2}$CD=$\sqrt{3}$,由勾股定理求出OH,求出∠COH=60°,由圆周角定理得出∠OAC=30°,OF=$\frac{1}{2}$OA=1,得出AC=2AF=2$\sqrt{3}$即可;
(2)延长OF交⊙O于M点,由OF=1,得出MF=1;另外过O点作AC的平行线交⊙O于点N、K,由OF=1,得出点N、K到直线AC的距离为1,即可得出结果.
解答 解:(1)作OF⊥AC于F,连接OC,如图1所示: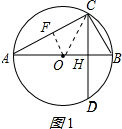
则AF=CF,
∵CD⊥AB于H,∴CH=DH=$\frac{1}{2}$CD=$\sqrt{3}$,
在Rt△OCH中,
∵OH=$\sqrt{{2}^{2}-(\sqrt{3})^{2}}$=1,
∴∠OCH=30°,∠COH=60°,
∴∠OAC=30°,
∴OF=$\frac{1}{2}$OA=1,
∴AC=2AF=2$\sqrt{{2}^{2}-{1}^{2}}$=2$\sqrt{3}$;
(2)此圆周上到直线AC的距离为1的点共有三个,理由如下:
如2图所示: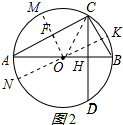
其一是延长OF交⊙O于M点,
∵OF=1,
∴MF=1;
另外过O点作AC的平行线交⊙O于点N、K,
∵OF=1,
∴点N、K到直线AC的距离为1.
点评 本题考查了垂径定理、勾股定理、含30°角的直角三角形的性质、圆周角定理等知识;熟练掌握垂径定理和圆周角定理,运用勾股定理进行计算是解决问题的关键.

练习册系列答案
相关题目
6.下列方程的变形,符合等式性质的是( )
| A. | 由2x-3=7得2x=7-3 | B. | 由2x-3=x-1得2x-1=x-3 | ||
| C. | 由-3x=5得x=5+3 | D. | 由-$\frac{1}{4}$x=1得x=-4 |
10.下列说法中正确的是( )
| A. | 在等式ax=bx两边除以x,可得a=b | B. | 由等式a2=b2,一定有a=b | ||
| C. | 在等式$\frac{a}{3}=\frac{b}{3}$两边除以3,得到a=b | D. | 由等式5x=4x+1,可得x=1 |