题目内容
17. 如图,在平行四边形ABCD中,M、N分别是BC、DC的中点,AM=4,AN=3,且∠MAN=60°,则AB的长是$\frac{14}{3}$.
如图,在平行四边形ABCD中,M、N分别是BC、DC的中点,AM=4,AN=3,且∠MAN=60°,则AB的长是$\frac{14}{3}$.
分析 首先延长DC和AM交于E,过点E作EH⊥AN于点H,易证得△ABM≌△ECM,即可得AB=$\frac{2}{3}$NE,然后由AM=4,AN=3,且∠MAN=60°,求得AH,NH与EH的长,继而求得EN的长,则可求得答案.
解答 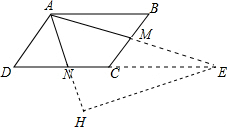 解:延长DC和AM交于E,过点E作EH⊥AN于点H,如图.
解:延长DC和AM交于E,过点E作EH⊥AN于点H,如图.
∵四边形ABCD为平行四边形,
∴AB∥CE,
∴∠BAM=∠CEM,∠B=∠ECM.
∵M为BC的中点,
∴BM=CM.
在△ABM和△ECM中,
$\left\{\begin{array}{l}{∠BAM=∠CEM}\\{∠B=∠ECM}\\{BM=CM}\end{array}\right.$,
∴△ABM≌△ECM(AAS),
∴AB=CD=CE,AM=EM=4,
∵N为边DC的中点,
∴NE=3NC=$\frac{3}{2}$AB,即AB=$\frac{2}{3}$NE,
∵AN=3,AE=2AM=8,且∠MAN=60°,
∴∠AEH=30°,
∴AH=$\frac{1}{2}$AE=4,
∴EH=$\sqrt{A{E}^{2}-A{H}^{2}}$=4$\sqrt{3}$,
∴NH=AH-AN=4-3=1,
∴EN=$\sqrt{N{H}^{2}+E{H}^{2}}$=7,
∴AB=$\frac{2}{3}$×7=$\frac{14}{3}$.
故答案为$\frac{14}{3}$.
点评 此题考查了平行四边形的性质、全等三角形的判定与性质以及勾股定理.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.在四个实数$\frac{3}{2}$,0,-1,$\sqrt{3}$中,最大的是( )
| A. | $\frac{3}{2}$ | B. | 0 | C. | -1 | D. | $\sqrt{3}$ |
 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于E,交BC边于F,分别连接AF和CE,AE=10.
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于E,交BC边于F,分别连接AF和CE,AE=10.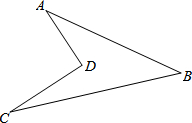 如图所示的一块土地,∠ADC=90°,AD=3m,CD=4m,AB=12m,BC=13m,求这块土地的面积.
如图所示的一块土地,∠ADC=90°,AD=3m,CD=4m,AB=12m,BC=13m,求这块土地的面积.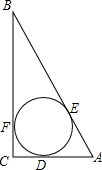 如图,⊙O为Rt△ABC的内切圆,⊙O的半径r=1,∠B=30°,
如图,⊙O为Rt△ABC的内切圆,⊙O的半径r=1,∠B=30°,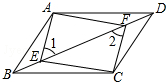 如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,BE=DF.
如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,BE=DF.