题目内容
1.解方程组:(1)$\left\{\begin{array}{l}{3x-5y=6}\\{x+4y=-15}\end{array}\right.$
(2)$\left\{\begin{array}{l}{\frac{x+y}{2}+\frac{x-y}{3}=1}\\{4(x+y)-5(x-y)=2}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{3x-5y=6①}\\{x+4y=-15②}\end{array}\right.$,
②×3-①得:17y=-51,即y=-3,
把y=-3代入②得:x=-3,
则方程组的解为$\left\{\begin{array}{l}{x=-3}\\{y=-3}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{5x+y=6①}\\{-x+9y=2②}\end{array}\right.$,
①+②×5得:46y=16,即y=$\frac{8}{23}$,
把y=$\frac{8}{23}$代入②得:x=$\frac{26}{23}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{26}{23}}\\{y=\frac{8}{23}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.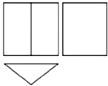 一个几何体的三视图如图所示,那么这个几何体是( )
一个几何体的三视图如图所示,那么这个几何体是( )
 一个几何体的三视图如图所示,那么这个几何体是( )
一个几何体的三视图如图所示,那么这个几何体是( )| A. | 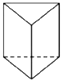 | B. | 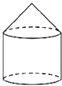 | C. | 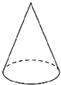 | D. | 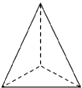 |
6.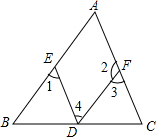 如图,在下列给出的条件中,不能判定AB∥DF的是( )
如图,在下列给出的条件中,不能判定AB∥DF的是( )
 如图,在下列给出的条件中,不能判定AB∥DF的是( )
如图,在下列给出的条件中,不能判定AB∥DF的是( )| A. | ∠A+∠2=180° | B. | ∠1=∠A | C. | ∠1=∠4 | D. | ∠A=∠3 |
9.观察下表:
(1)结合该表格及相关知识,求x,y;
(2)猜想第n行的三个数(用含n的式子表示),并证明它们是一组勾股数.
| 4 | 3 | 5 | 32+42=52 |
| 6 | 8 | 10 | 62+82=102 |
| 8 | 15 | 17 | 82+152=172 |
| 10 | 24 | 26 | 102+242=262 |
| … | … | … | … |
| 60 | x | y | 602+x2=y2 |
| … | … | … | … |
(2)猜想第n行的三个数(用含n的式子表示),并证明它们是一组勾股数.