题目内容

16．解方程组：$\left\{\begin{array}{l}{x-\frac{y}{3}=1}\\{2（x-4）+3y=5}\end{array}\right.$．

分析 方程组整理后，利用加减消元法求出解即可．

解答 解：原方程组可化为$\left\{\begin{array}{l}{3x-y=3①}\\{2x+3y=13②}\end{array}\right.$，
①×3+②，得11x=22，即x=2，
将x=2代入①，得6-y=3，即y=3，
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$．

点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．

练习册系列答案
相关题目
9．中国钓鱼岛列岛8个小岛之一的飞濑岛的面积为0.0008平方公里，仅仅只有武进吾悦广场占地面积的$\frac{1}{225}$．用科学记数法表示飞濑岛的面积约为8×10-4平方公里．
8．2015年9月3日在北京举行了中国人民抗日战争暨世界反法西斯战争胜利70周年纪念活动，正式受阅12000人．将12000用科学记数法表示正确的是（　　）
A．12×104B．1.2×105C．1.2×104D．0.12×104
4．某校对甲、乙两名跳高运动员的10次跳高成绩进行统计分析，结果如下：甲和乙的平均跳高成绩分别为$\overline{x}$甲=1.69m，$\overline{x}$乙=1.69m，方差为S甲2=0.0006，S乙2=0.00315，则这两名运动员中甲的成绩更稳定（填甲或乙）
11．函数y=$\frac{x+3}{\sqrt{x-2}}$中，自变量x的取值范围是（　　）
A．x＞2B．x＞2且x≠-3C．x＞-3D．x≥-3且x≠2
1．解方程组：
（1）$\left\{\begin{array}{l}{3x-5y=6}\\{x+4y=-15}\end{array}\right.$                      
（2）$\left\{\begin{array}{l}{\frac{x+y}{2}+\frac{x-y}{3}=1}\\{4（x+y）-5（x-y）=2}\end{array}\right.$．
8．计算（-2016）0的值为1．
5．中国汉字博大精深，结构有趣，为弘扬中华汉字文化，九（1）班举行了一次汉字拼接游戏，游戏规则是：如图，将五张卡片正面分别写上“亻”“阝”“又”“日”“十”（除正面上的部首或文字不同外，卡片的材质和大小均相同），洗匀后放在一个不透明的箱子里，每人随机地从箱子里连续摸取两张卡片，若这两张卡片上的部首或文字能重新组成一个汉字，则可获得一份奖品．
请回答下列问题：
（1）随机地从箱子里连续摸取两张卡片，可能的结果有哪些？（请用画树状图或列表法求解）
（2）在这个游戏中，获得奖品的概率是多少？

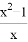先化简： （1+）÷，再从1、-1、0、2中选择一个合适的数代入求值：

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网