题目内容
4.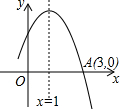 如图所示是二次函数y=ax2+bx+c图象的一部分,图象过A点(3,0),对称轴为x=1,给出四个结论:①b2-4ac>0;②2a+b=0;③a+b=0;④当x=-1或x=3时,函数y的值都等于0,其中正确结论是( )
如图所示是二次函数y=ax2+bx+c图象的一部分,图象过A点(3,0),对称轴为x=1,给出四个结论:①b2-4ac>0;②2a+b=0;③a+b=0;④当x=-1或x=3时,函数y的值都等于0,其中正确结论是( )| A. | ②③④ | B. | ①③④ | C. | ①②③ | D. | ①②④ |
分析 首先根据二次函数y=ax2+bx+c图象与x轴有两个交点,可得△>0,所以b2-4ac>0;然后根据图象过A点(3,0),对称轴为x=1,可得图象与x轴的另一个交点是(-1,0),所以当x=-1或x=3时,函数y的值都等于0;最后根据图象过A点(3,0),(-1,0),可得9a+3b+c=0,a-b+c=0,据此判断出2a+b=0即可.
解答 解:∵二次函数y=ax2+bx+c图象与x轴有两个交点,
∴△>0,
∴b2-4ac>0,
∴①正确;
∵图象过A点(3,0),对称轴为x=1,
∴图象与x轴的另一个交点是(-1,0),
∴当x=-1或x=3时,函数y的值都等于0,
∴④正确;
∵图象过A点(3,0),(-1,0),
∴9a+3b+c=0,a-b+c=0,
整理,可得2a+b=0,
∴②正确,③不正确.
综上,可得
正确结论是:①②④.
故选:D.
点评 此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).

练习册系列答案
相关题目
14.圆锥的底面半径为3,高为4,则圆锥侧面展开图的面积为( )
| A. | 5π | B. | 10π | C. | 15π | D. | 20π |
13.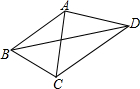 如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )
如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )
 如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )
如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )| A. | 68° | B. | 88° | C. | 90° | D. | 112° |
14.某超市预购进A、B两种品牌的T恤共200件,已知两种T恤的进价如表所示,设购进A种T恤x件,且所购进的两种T恤全部卖出,获得的总利润为W元.
(1)求W关于x的函数关系式;
(2)如果购进两种T恤的总费用不超过9500元,那么超市如何进货才能获得最大利润?并求出最大利润.(提示:利润=售价-进价)
| 品牌 | 进价/(元/件) | 售价/(元/件) |
| A | 50 | 80 |
| B | 40 | 65 |
(2)如果购进两种T恤的总费用不超过9500元,那么超市如何进货才能获得最大利润?并求出最大利润.(提示:利润=售价-进价)
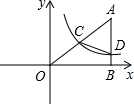 如图,在平面直角坐标系中A点的坐标为(8,y),AB⊥x轴于点B,sin∠OAB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$的图象的一支经过AO的中点C,且与AB交于点D.
如图,在平面直角坐标系中A点的坐标为(8,y),AB⊥x轴于点B,sin∠OAB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$的图象的一支经过AO的中点C,且与AB交于点D.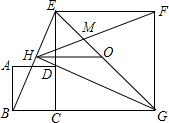 如图,正方形ABCD的边CD在正方形ECGF的边CE上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH,FH,EG与FH交于点M,对于下面四个结论:①GH⊥BE;②HO$\stackrel{∥}{=}$$\frac{1}{2}$BG;③S正方形ABCD:S正方形ECGF=1:$\sqrt{2}$;④EM:MG=1:(1+$\sqrt{2}$),其中正确结论的序号为①②④.
如图,正方形ABCD的边CD在正方形ECGF的边CE上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH,FH,EG与FH交于点M,对于下面四个结论:①GH⊥BE;②HO$\stackrel{∥}{=}$$\frac{1}{2}$BG;③S正方形ABCD:S正方形ECGF=1:$\sqrt{2}$;④EM:MG=1:(1+$\sqrt{2}$),其中正确结论的序号为①②④. 如图,在正六边形ABCDEF中,连接对角线AC,CE,DF,EA,FB,可以得到一个六角星.记这些对角线的交点分别为H,I,J,K,L、M,则图中等边三角形共有8个.
如图,在正六边形ABCDEF中,连接对角线AC,CE,DF,EA,FB,可以得到一个六角星.记这些对角线的交点分别为H,I,J,K,L、M,则图中等边三角形共有8个.