题目内容
1. 如图,△ABC是圆O的内接等腰三角形,AB=CB,AD是直径,∠DAC=40°,求∠BAD的度数.
如图,△ABC是圆O的内接等腰三角形,AB=CB,AD是直径,∠DAC=40°,求∠BAD的度数.
分析 由AB=AC,推出$\widehat{AB}$=$\widehat{AC}$,推出AD⊥BC(垂径定理),推出∠DAB=∠DAC(三线合一),即可解决问题.
解答 解: ∵AB=AC,
∵AB=AC,
∴$\widehat{AB}$=$\widehat{AC}$,
∴AD⊥BC(垂径定理),
∴∠DAB=∠DAC(三线合一),
∵∠DAC=40°,
∴∠BAD=40°.
点评 本题考查三角形的外接圆于外心、等腰三角形的性质、垂径定理等知识,解题的关键是灵活运用所学知识,属于基础题,中考常考题型.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
10.已知三角形三边长分别为3、x、10,若x为正整数,则这样的三角形个数为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 如图,AC∥DE,CD平分∠ACB,EF平分∠DEB,猜想∠CDE与∠DEF的关系并加以证明.
如图,AC∥DE,CD平分∠ACB,EF平分∠DEB,猜想∠CDE与∠DEF的关系并加以证明.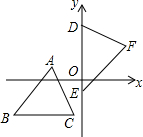 如图,直角坐标平面上,△ABC与△DEF全等,其中A,B,C的对应顶点分别为D,E,F,且AB=BC=5.若A点的坐标为(-3,1),B,C两点纵坐标都是-3,D,E两点在y轴上,则F点到y轴的距离为4.
如图,直角坐标平面上,△ABC与△DEF全等,其中A,B,C的对应顶点分别为D,E,F,且AB=BC=5.若A点的坐标为(-3,1),B,C两点纵坐标都是-3,D,E两点在y轴上,则F点到y轴的距离为4.