题目内容
9. 如图,AC∥DE,CD平分∠ACB,EF平分∠DEB,猜想∠CDE与∠DEF的关系并加以证明.
如图,AC∥DE,CD平分∠ACB,EF平分∠DEB,猜想∠CDE与∠DEF的关系并加以证明.
分析 根据平行线的性质,得出∠ACB=∠DEB,∠ACD=∠CDE,再根据角平分线的定义,得到∠ACD=$\frac{1}{2}$∠ACB=$\frac{1}{2}$∠DEB=∠DEF,即可得到∠CDE=∠DEF.
解答 解:∠CDE=∠DEF.
证明:∵AC∥DE,
∴∠ACB=∠DEB,∠ACD=∠CDE,
∵CD平分∠ACB,EF平分∠DEB,
∴∠ACD=$\frac{1}{2}$∠ACB=$\frac{1}{2}$∠DEB=∠DEF,
∴∠CDE=∠DEF.
点评 本题主要考查了平行线的性质以及角平分线的定义的运用,解决问题的关键是掌握:两直线平行,同位角相等;两直线平行,内错角相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
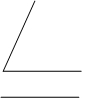 (1)如图,已知∠α和线段a,用尺规作图作△ABC,使AB=AC=a,∠B=∠α.
(1)如图,已知∠α和线段a,用尺规作图作△ABC,使AB=AC=a,∠B=∠α.
 用10米长的铝合金做成一个长方形的窗框(如图),设长方形窗框的横条长度为x米,则长方形窗框的面积为x(5-1.5x)平方米.
用10米长的铝合金做成一个长方形的窗框(如图),设长方形窗框的横条长度为x米,则长方形窗框的面积为x(5-1.5x)平方米. 如图,△ABC是圆O的内接等腰三角形,AB=CB,AD是直径,∠DAC=40°,求∠BAD的度数.
如图,△ABC是圆O的内接等腰三角形,AB=CB,AD是直径,∠DAC=40°,求∠BAD的度数.