题目内容
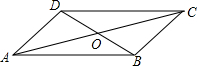 如图,在平行四边形ABCD中,AB:BC=5:4,对角线AC,BC相交于点O,且BC⊥BD,BC=6,试求AB、AC的长.
如图,在平行四边形ABCD中,AB:BC=5:4,对角线AC,BC相交于点O,且BC⊥BD,BC=6,试求AB、AC的长.考点:平行四边形的性质
专题:
分析:先由AB:BC=5:4,BC=6,求出AB=
=7.5.再设OB=x,OC=y,根据平行四边形的性质及已知BC⊥BD,得出BD=2OB=2x,AC=2OC=2y,∠ADB=∠DBC=90°,AD=BC=6.在Rt△OBC中,由勾股定理得出x2+62=y2 ①,在Rt△ADB中,由勾股定理得出(2x)2+62=7.52 ,解方程求出x=2.25,把x=2.25代入①,求出y的值,进而求出AC.
| 5BC |
| 4 |
解答:解:∵AB:BC=5:4,BC=6,
∴AB=
=7.5.
设OB=x,OC=y,
∵在平行四边形ABCD中,对角线AC,BC相交于点O,BC⊥BD,
∴BD=2OB=2x,AC=2OC=2y,∠ADB=∠DBC=90°,AD=BC=6.
在Rt△OBC中,∵∠OBC=90°,
∴OB2+BC2=OC2,即x2+62=y2 ①,
在Rt△ADB中,∵∠ADB=90°,
∴BD2+AD2=AB2,即(2x)2+62=7.52 ,
解得x=±2.25(负值舍去),
把x=2.25代入①,得2.252+62=y2 ,
解得y=±
(负值舍去),
∴AC=2y=
.
故AB=7.5,AC=
.
∴AB=
| 5BC |
| 4 |
设OB=x,OC=y,
∵在平行四边形ABCD中,对角线AC,BC相交于点O,BC⊥BD,
∴BD=2OB=2x,AC=2OC=2y,∠ADB=∠DBC=90°,AD=BC=6.
在Rt△OBC中,∵∠OBC=90°,
∴OB2+BC2=OC2,即x2+62=y2 ①,
在Rt△ADB中,∵∠ADB=90°,
∴BD2+AD2=AB2,即(2x)2+62=7.52 ,
解得x=±2.25(负值舍去),
把x=2.25代入①,得2.252+62=y2 ,
解得y=±
3
| ||
| 4 |
∴AC=2y=
3
| ||
| 2 |
故AB=7.5,AC=
3
| ||
| 2 |
点评:本题考查了平行四边形的性质,勾股定理,比例的性质,难度适中.正确求出OB的长是解题的关键.

练习册系列答案
相关题目
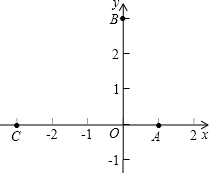 如图,已知点A(1,0),B(0,3),C(-3,0),动点P(x,y)在线段AB上,CP交y轴于点D,设BD的长为t.
如图,已知点A(1,0),B(0,3),C(-3,0),动点P(x,y)在线段AB上,CP交y轴于点D,设BD的长为t. 小明从黄山百步云梯脚下的点A约走了50m后,到达山顶的点B.已知山顶B到山脚下的垂直距离约是30m,求山坡的坡度.
小明从黄山百步云梯脚下的点A约走了50m后,到达山顶的点B.已知山顶B到山脚下的垂直距离约是30m,求山坡的坡度. 若在△ABC中,∠C=90°,以AC为直径的⊙O与边AB相交于点D,AC=4cm,BC=3cm,则点O到AB的距离为
若在△ABC中,∠C=90°,以AC为直径的⊙O与边AB相交于点D,AC=4cm,BC=3cm,则点O到AB的距离为