题目内容
若在△ABC中，∠C=90°，以AC为直径的⊙O与边AB相交于点D，AC=4cm，BC=3cm，则点O到AB的距离为考点：直线与圆的位置关系,勾股定理,三角形中位线定理
专题：
分析：作OD⊥AB于点D，由勾股定理可得AB=5，根据∠C=90°，得到△AOE∽△ABC，然后利用相似三角形的对应边的比相等列出方程求解即可．
解答：
解：作OE⊥AB于点E，由勾股定理可得AB=5，
∵∠C=90°，
∴△AOE∽△ABC，
∴
=
，
即：
=
，
∴OE=
，
即点O到AB的距离为
．
解：作OE⊥AB于点E，由勾股定理可得AB=5，∵∠C=90°，
∴△AOE∽△ABC，
∴
| OE |
| BC |
| AO |
| AB |
即：
| OE |
| 3 |
| 2 |
| 5 |
∴OE=
| 6 |
| 5 |
即点O到AB的距离为
| 6 |
| 5 |
点评：本题考查了直线与圆的位置关系，解题的关键是得到相似三角形，难度不大．
练习册系列答案
通城学典默写能手系列答案
相关题目
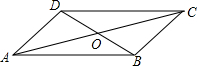如图，在平行四边形ABCD中，AB：BC=5：4，对角线AC，BC相交于点O，且BC⊥BD，BC=6，试求AB、AC的长．
二次函数y=ax2+bx+c的图象如图所示，则a
如图，在△ABC中，AB=AC=5，BC=6，点M为BC中点，N为AC上一动点，则MN的长的范围为
已知有理数a，b在数轴上对应的位置如图所示，化简：|b-a|-|a+b|+|a|=下列句子中是命题的是（ ）
①三个角对应相等的两个三角形全等 ②负数都小于0
③过直线l外一点作l的平行线 ④a＞b，a＞c，那么a=c．
①三个角对应相等的两个三角形全等 ②负数都小于0
③过直线l外一点作l的平行线 ④a＞b，a＞c，那么a=c．
| A、② | B、②③④ | C、②④ | D、①②④ |