题目内容
16.已知二次函数的解析式为y=ax2+bx+c(a、b、c为常数,a≠0),且a2+ab+ac<0,下列说法:①b2-4ac<0;
②ab+ac<0;
③方程ax2+bx+c=0有两个不同根x1、x2,且(x1-1)(1-x2)>0;
④二次函数的图象与坐标轴有三个不同交点,
其中正确的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据题意把a的符号分成两种情况,再由a2+ab+ac<0判断出a+b+c的符号,即可得出当x=1时,y的符号,从而得出b+c的符号,再得出方程ax2+bx+c=0有一个根大于1,一个根小于1,即可得出(x1-1)(x2-1)<0;b2-4ac>0;抛物线和坐标轴有二个交点.
解答 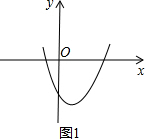 解:当a>0时,
解:当a>0时,
∵a2+ab+ac<0,
∴a+b+c<0,
∴b+c<0,
如图1,
∴b2-4ac>0,故①错误;
a(b+c)<0,故②正确;
∴方程ax2+bx+c=0有两个不同根x1、x2,且x1<1,x2>1,
∴(x1-1)(x2-1)<0,
即(x1-1)(1-x2)>0,故③正确;
∴二次函数的图象与坐标轴有二个不同交点,故④错误;
故选B.
点评 本题考查了二次函数的图象与系数的关系,掌握分类讨论思想是解题的关键.

练习册系列答案
相关题目
6.$-1\frac{1}{2}$的倒数是( )
| A. | 1$\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | -1$\frac{1}{2}$ | D. | -$\frac{2}{3}$ |
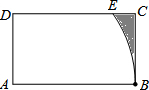 如图,在矩形ABCD中,AB=4,AD=2,以点A为圆心,AB长为半径画圆弧交边DC于点E,则阴影部分的面积是8-2$\sqrt{3}$-$\frac{4π}{3}$(结果保留π).
如图,在矩形ABCD中,AB=4,AD=2,以点A为圆心,AB长为半径画圆弧交边DC于点E,则阴影部分的面积是8-2$\sqrt{3}$-$\frac{4π}{3}$(结果保留π). 如图,AC⊥CB,DB⊥CB,垂足分别为C、B,AB=DC,求证:∠ABD=∠ACD.
如图,AC⊥CB,DB⊥CB,垂足分别为C、B,AB=DC,求证:∠ABD=∠ACD. 如图,已知△ABC≌△DBE,如果∠CBD=96°,∠CBE=28°,那么∠ABC=68°.
如图,已知△ABC≌△DBE,如果∠CBD=96°,∠CBE=28°,那么∠ABC=68°.