题目内容
14. 已知矩形ABCD中,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,且四边形EFDC与矩形ABCD相似.
已知矩形ABCD中,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,且四边形EFDC与矩形ABCD相似.(1)求证:四边形ABEF是正方形;
(2)求证:F点是AD的黄金分割点.
分析 (1)根据题意证明四边形ABEF是矩形,根据折叠的性质得到AB=AF,证明结论;
(2)根据相似多边形的性质得到AB2=FD•AB,根据正方形的性质得到答案.
解答 证明:(1)∵∠B=∠BAF=∠AFE=90°,
∴四边形ABEF是矩形,
由折叠的性质可知AB=AF,
∴四边形ABEF是正方形;
(2)∵四边形EFDC与矩形ABCD相似
∴$\frac{FD}{AB}$=$\frac{CD}{AD}$,又AB=CD,
∴AB2=FD•AB,又AB=AF,
∴AF2=FD•AB,
∴F点是AD的黄金分割点.
点评 本题考查的是相似多边形的性质和黄金分割的概念,掌握相似多边形的性质为:对应角相等;对应边的比相等是解题的关键,注意把线段分成两条线段,且使较长是已知线段和较短的比例中项,叫做把线段AB黄金分割.

练习册系列答案
相关题目
4.一个有理数的相反数与这个有理数的绝对值的和( )
| A. | 可能是负数 | B. | 是正数 | C. | 是正数或者是零 | D. | 是零 |
6.$-1\frac{1}{2}$的倒数是( )
| A. | 1$\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | -1$\frac{1}{2}$ | D. | -$\frac{2}{3}$ |
 画出△ABC关于直线MN对称的△A1B1C1.
画出△ABC关于直线MN对称的△A1B1C1.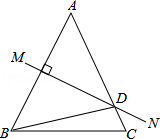 如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠C的度数是65°.
如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠C的度数是65°.