题目内容
在Rt△ABC,∠ACB=90°,AC=4,BC=3,以C为圆心的⊙C与斜边AB相切,则⊙C的半径为 .
考点:直线与圆的位置关系
专题:计算题
分析:作CD⊥AB于D,在Rt△ACB中,根据勾股定理计算出AB=5,再利用面积法计算出CD=
,然后根据直线和圆的位置关系得到以C为圆心的⊙C与斜边AB相切时,⊙C的半径等于CD的长.
| 12 |
| 5 |
解答:解: 作CD⊥AB于D,如图,
作CD⊥AB于D,如图,
在Rt△ACB中,
∵AC=4,BC=3,
∴AB=
=5,
∵S△ABC=
AC•BC=
•AB•CD,
∴CD=
=
,
∵以C为圆心的⊙C与斜边AB相切,
∴⊙C的半径等于CD的长,
即⊙C的半径为
.
故答案为
.
 作CD⊥AB于D,如图,
作CD⊥AB于D,如图,在Rt△ACB中,
∵AC=4,BC=3,
∴AB=
| AC2+BC2 |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=
| 3×4 |
| 5 |
| 12 |
| 5 |
∵以C为圆心的⊙C与斜边AB相切,
∴⊙C的半径等于CD的长,
即⊙C的半径为
| 12 |
| 5 |
故答案为
| 12 |
| 5 |
点评:本题考查了直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d:直线l和⊙O相交?d<r;直线l和⊙O相切?d=r;直线l和⊙O相离?d>r.也考查了勾股定理.

练习册系列答案
相关题目
已知⊙O1的半径为2cm,⊙O2的半径为3cm,且O1O2=1cm,则⊙O1和⊙O2的位置关系为( )
| A、内切 | B、相交 | C、外切 | D、外离 |
 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图,已知EF=CD=80cm,则截面圆的半径为
把球放在长方体纸盒内,球的一部分露出盒外,其截面如图,已知EF=CD=80cm,则截面圆的半径为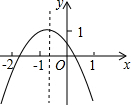 二次函数y=ax2+bx+c(a≠0)的图象如图,若M=a+b-c,N=4a-2b+c,P=2a-b,Q=b2-4ac.则M,N,P,Q中,值小于0的数有
二次函数y=ax2+bx+c(a≠0)的图象如图,若M=a+b-c,N=4a-2b+c,P=2a-b,Q=b2-4ac.则M,N,P,Q中,值小于0的数有