题目内容
 如图,当太阳在A处时,小明测得某树的影长为2米,当太阳在B处时又测得该树的影长为8米.若两次日照的光线互相垂直,则这颗树的高度为
如图,当太阳在A处时,小明测得某树的影长为2米,当太阳在B处时又测得该树的影长为8米.若两次日照的光线互相垂直,则这颗树的高度为考点:相似三角形的应用,平行投影
专题:
分析:在图形标注字母,然后求出△CDE和△FDC相似,根据相似三角形对应边成比例可得
=
,然后代入数据进行计算即可得解.
| CD |
| DF |
| DE |
| CD |
解答: 解:如图,∵两次日照的光线互相垂直,
解:如图,∵两次日照的光线互相垂直,
∴∠E+∠F=90°,∠E+∠ECD=90°,
∴∠ECD=∠F,
又∵∠CDE=∠FDC=90°,
∴△CDE∽△FDC,
∴
=
,
由题意得,DE=2,DF=8,
∴
=
,
解得CD=4,
即这颗树的高度为4米.
故答案为:4.
 解:如图,∵两次日照的光线互相垂直,
解:如图,∵两次日照的光线互相垂直,∴∠E+∠F=90°,∠E+∠ECD=90°,
∴∠ECD=∠F,
又∵∠CDE=∠FDC=90°,
∴△CDE∽△FDC,
∴
| CD |
| DF |
| DE |
| CD |
由题意得,DE=2,DF=8,
∴
| CD |
| 8 |
| 2 |
| CD |
解得CD=4,
即这颗树的高度为4米.
故答案为:4.
点评:本题考查了相似三角形的应用,平行投影,确定出相似三角形是解题的关键,标注字母更便于叙述.

练习册系列答案
相关题目
2的相反数是( )
A、-
| ||
B、
| ||
| C、2 | ||
| D、-2 |
 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图,已知EF=CD=80cm,则截面圆的半径为
把球放在长方体纸盒内,球的一部分露出盒外,其截面如图,已知EF=CD=80cm,则截面圆的半径为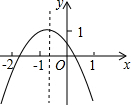 二次函数y=ax2+bx+c(a≠0)的图象如图,若M=a+b-c,N=4a-2b+c,P=2a-b,Q=b2-4ac.则M,N,P,Q中,值小于0的数有
二次函数y=ax2+bx+c(a≠0)的图象如图,若M=a+b-c,N=4a-2b+c,P=2a-b,Q=b2-4ac.则M,N,P,Q中,值小于0的数有 如图,在⊙O中,弦BC=1,点A是圆上一点,且∠BAC=30°,则⊙O的半径是
如图,在⊙O中,弦BC=1,点A是圆上一点,且∠BAC=30°,则⊙O的半径是 如图,在正方形网格中,tanC=
如图,在正方形网格中,tanC=