题目内容
10.某仓储系统有12条输入传送带,12条输出传送带.某日,控制室的电脑显示,每条输入传送带每小时进库的货物流量如图1,每条输出传送带每小时出库的货物流量如图2,而该日仓库中原有货物8吨,在0时至5时,仓库中货物存量变化情况如图3.
(1)每条输入传送带每小时进库的货物流量为13吨,每条输出传送带每小时出库的货物流量为15吨.
(2)在0时至2时内,求出仓库内货物存量y(吨)与时间x(小时)之间的函数关系式:y=2x+8.
(3)在4时至5时,有6条输入传送带和6条输出传送带在工作.
分析 (1)根据“每小时传送货物量=增加(减少)的量÷时间”结合图1和图2即可得出结论;
(2)设函数关系式为y=kx+b,由图3找出点的坐标,利用待定系数法即可求出结论;
(3)设在4时至5时,有m条输入传送带和n条输出传送带在工作.结合图象得出15n-13m=12,结合m、n的取值范围即可得出结论.
解答 解:(1)每条输入传送带每小时进库的货物流量为:13÷1=13(吨),
每条输出传送带每小时出库的货物流量为15÷1=15(吨).
故答案为:13;15.
(2)当0≤x≤2时,设函数关系式为y=kx+b,
∵函数的图象过点(0,8),(2,12),
∴有$\left\{\begin{array}{l}{2k+b=12}\\{b=8}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=2}\\{b=8}\end{array}\right.$.
∴y=2x+8(0≤x≤2).
故答案为:y=2x+8.
(3)设在4时至5时,有m条输入传送带和n条输出传送带在工作.
由题意得:15n-13m=12.
∴n=$\frac{13m+12}{15}$.
∵0≤m≤12,且m和n均为整数,
∴13m+12为15的整数倍,
∴m=6,此时n=6.
故答案为:6;6.
点评 本题考查了一次函数的应用以及待定系数法求函数解析式,解题的关键是:(1)根据数量关系直接求值;(2)找出点的坐标利用待定系数法求出函数关系式;(3)根据数量关系得出关于m、n的方程,结合m、n的范围找出结论.本题属于基础题,难度不大,解决该题型题目时,根据数量关系结合图象找出方程(或方程组)是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.等腰三角形三边长分别为a、b、4,且a、b是关于x的一元二次方程x2-12x+k+2=0的两根,则k的值为( )
| A. | 30 | B. | 34或30 | C. | 36或30 | D. | 34 |
2.方程组$\left\{\begin{array}{l}{x-y=1}\\{x+y=3}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |

 如图,一次函数y=-$\frac{4}{5}$x+12与x轴、y轴相交于点A、B两点,动点P以4个单位/秒的速度从点O出发,沿OA方向在线段OA上运动,以P为圆心,OP长为半径作⊙P;同时动点E以5个单位/秒的速度从点A出发,沿x轴的负半轴方向运动,过点E作EF⊥x轴,交射线AB于点F,以EF为边在EF的左侧作正方形EFMN,设运动时间为t秒.
如图,一次函数y=-$\frac{4}{5}$x+12与x轴、y轴相交于点A、B两点,动点P以4个单位/秒的速度从点O出发,沿OA方向在线段OA上运动,以P为圆心,OP长为半径作⊙P;同时动点E以5个单位/秒的速度从点A出发,沿x轴的负半轴方向运动,过点E作EF⊥x轴,交射线AB于点F,以EF为边在EF的左侧作正方形EFMN,设运动时间为t秒.
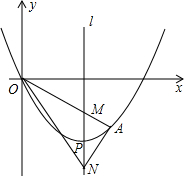 如图,抛物线y=$\frac{1}{4}$(x-4)2-4的顶点为P,M,N均在对称轴上,且PM=PN,延长OM交抛物线于点A,求证:∠ANM=∠ONM.
如图,抛物线y=$\frac{1}{4}$(x-4)2-4的顶点为P,M,N均在对称轴上,且PM=PN,延长OM交抛物线于点A,求证:∠ANM=∠ONM.