题目内容
某电脑公司要往甲校送8台电脑,往乙校送10台电脑,但现在仅有12台电脑,需要到总公司调运6台电脑.从电脑公司运一台到甲、乙两校的费用分别为30元和50元.从总公司调运一台电脑到甲、乙两校的费用分别是40元和80元.若要求总运费不超过840元,共有几种调运方案?请你设计出运费最低的方案.
考点:一元一次不等式组的应用
专题:
分析:求出总费用关于从合肥送到某个县的台数的函数关系式,再根据函数的增减性质和自变量的取值范围求出答案.
解答:解:设电脑公司要往甲校送x台电脑,总运费y元,
则往乙校送(10-x)台、运往祁门县(x+2),从合肥运往祁门县(6-x)台,
所以,y=40x+80(6-x)+30(10-x)+50(x+2),
即:y=-20x+880(0≤x≤6)y随x增大而减小,
所以x最大为6时,760值最小,此时10-x=4,x+2=8,6-x=0,
即从合肥运往黟县6台,从教委运往黟县4台,运往祁门县8台时,总费用最低,为760元.
则往乙校送(10-x)台、运往祁门县(x+2),从合肥运往祁门县(6-x)台,
所以,y=40x+80(6-x)+30(10-x)+50(x+2),
即:y=-20x+880(0≤x≤6)y随x增大而减小,
所以x最大为6时,760值最小,此时10-x=4,x+2=8,6-x=0,
即从合肥运往黟县6台,从教委运往黟县4台,运往祁门县8台时,总费用最低,为760元.
点评:利用一次函数求解实际问题,把复杂的实际问题转化成数学问题,学会运用各种方法求解析式,会运用一次函数的最大最小值来解决实际问题.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 已知AB∥ED,∠ABC=140°,∠BCD=80°,求∠CDE.
已知AB∥ED,∠ABC=140°,∠BCD=80°,求∠CDE.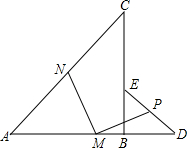 将等腰Rt△ABC和等腰Rt△BDE的直角顶点B重合,M、N、P分别是AD、AC、DE边的中点,且A、B、D在同一直线上,试说明MP与MN的关系.
将等腰Rt△ABC和等腰Rt△BDE的直角顶点B重合,M、N、P分别是AD、AC、DE边的中点,且A、B、D在同一直线上,试说明MP与MN的关系. 如图,三角形ABO的面积为12,且AO=AB,双曲线y=
如图,三角形ABO的面积为12,且AO=AB,双曲线y=