题目内容
2.正方形的面积是2,它的对角线长为( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
分析 由正方形的性质得出AC=BD,AC⊥BD,得出正方形的面积=$\frac{1}{2}$AC2=2,即可求出对角线AC的长.
解答 解:如图所示:
∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,
∴正方形的面积=$\frac{1}{2}$AC•BD=$\frac{1}{2}$AC2=2,
∴AC2=4,
∴AC=2,
故选:B.
点评 本题考查了正方形的性质、正方形面积的计算方法;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
12. 如图,已知A、B两点是反比例函数y=$\frac{2}{x}$(x>0)的图象上任意两点,过A、B两点分别作y轴的垂线,垂足分别是C、D.连接AB、AO、BO,则梯形ABDC的面积与△ABO的面积比是( )
如图,已知A、B两点是反比例函数y=$\frac{2}{x}$(x>0)的图象上任意两点,过A、B两点分别作y轴的垂线,垂足分别是C、D.连接AB、AO、BO,则梯形ABDC的面积与△ABO的面积比是( )
 如图,已知A、B两点是反比例函数y=$\frac{2}{x}$(x>0)的图象上任意两点,过A、B两点分别作y轴的垂线,垂足分别是C、D.连接AB、AO、BO,则梯形ABDC的面积与△ABO的面积比是( )
如图,已知A、B两点是反比例函数y=$\frac{2}{x}$(x>0)的图象上任意两点,过A、B两点分别作y轴的垂线,垂足分别是C、D.连接AB、AO、BO,则梯形ABDC的面积与△ABO的面积比是( )| A. | 2:1 | B. | 1:2 | C. | 1:1 | D. | 2:3 |
10.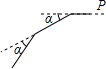 如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )
如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )
 如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )
如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )| A. | 30° | B. | 40° | C. | 80° | D. | 108° |
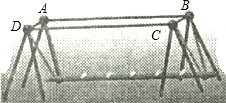 如图是一种儿童的游乐设施-儿童荡板.小明想验证这个荡板上方的四边形是否是平行四边形,现在手头只有一根足够长的绳子,请你帮助他设计一个验证方案,并说明理由.
如图是一种儿童的游乐设施-儿童荡板.小明想验证这个荡板上方的四边形是否是平行四边形,现在手头只有一根足够长的绳子,请你帮助他设计一个验证方案,并说明理由.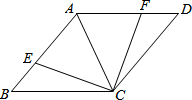 如图,AC是菱形ABCD的对角线,点E,F分别在AB,AD上,且AE=AF.求证:CE=CF.
如图,AC是菱形ABCD的对角线,点E,F分别在AB,AD上,且AE=AF.求证:CE=CF.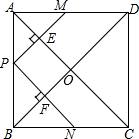 如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:
如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论: 如图,三条直线相交于点O,若CO⊥AB,∠1=56°,则∠2=34°.
如图,三条直线相交于点O,若CO⊥AB,∠1=56°,则∠2=34°.