题目内容
1. 在△ABC中,点D、E、F分别在BC、AB、AC上,BE=CF,△DEB与△DFC的面积相等.求证:AD平分∠BAC.
在△ABC中,点D、E、F分别在BC、AB、AC上,BE=CF,△DEB与△DFC的面积相等.求证:AD平分∠BAC.
分析 作DG⊥AB于G,DH⊥AC于H,根据三角形的面积公式求出DG=DH,根据到角的两边的距离相等的点在角的平分线上证明结论.
解答  证明:作DG⊥AB于G,DH⊥AC于H,
证明:作DG⊥AB于G,DH⊥AC于H,
∵△DEB与△DFC的面积相等,
∴$\frac{1}{2}$×BE×DG=$\frac{1}{2}$×FC×DH,又BE=CF,
∴DG=DH,
又∵DG⊥AB,DH⊥AC,
∴AD平分∠BAC.
点评 本题考查的是三角形的面积和角平分线的判定,掌握到角的两边的距离相等的点在角的平分线上是解题的关键.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
11.若方程组$\left\{\begin{array}{l}{ax+2y=1}\\{3x+y=2}\end{array}\right.$有唯一解,则a的取值范围为( )
| A. | a≠6 | B. | a=6 | C. | a≠4 | D. | a=4 |
9.下列各式中,不正确的是( )
| A. | |-0.2|>-0.2 | B. | -|-0.2|<-(-0.2) | C. | -|-0.2|>-0.2 | D. | |-0.2|>|-0.02| |
13.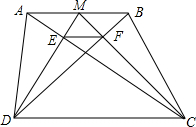 已知:如图,在梯形ABCD中,AB∥CD,M是AB的中点,分别连接AC、BD、MD、MC,且AC与MD交于点E,DB与MC交于F.
已知:如图,在梯形ABCD中,AB∥CD,M是AB的中点,分别连接AC、BD、MD、MC,且AC与MD交于点E,DB与MC交于F.
(1)求证:EF∥CD;
(2)若AB=a,CD=b,求EF的长.
 已知:如图,在梯形ABCD中,AB∥CD,M是AB的中点,分别连接AC、BD、MD、MC,且AC与MD交于点E,DB与MC交于F.
已知:如图,在梯形ABCD中,AB∥CD,M是AB的中点,分别连接AC、BD、MD、MC,且AC与MD交于点E,DB与MC交于F.(1)求证:EF∥CD;
(2)若AB=a,CD=b,求EF的长.
10.下列调查中,适宜采用普查方式的是( )
| A. | 调查某水库中鱼的种类 | |
| B. | 调查某市民对汽车废气污染环境的看法 | |
| C. | 调查某班同学的视力情况 | |
| D. | 调查某型号节能灯的使用寿命 |
11.下列各图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
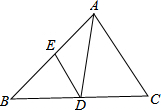 如图,AD平分∠BAC,DE∥AC,则△AED一定是等腰三角形.
如图,AD平分∠BAC,DE∥AC,则△AED一定是等腰三角形.