题目内容
13.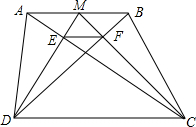 已知:如图,在梯形ABCD中,AB∥CD,M是AB的中点,分别连接AC、BD、MD、MC,且AC与MD交于点E,DB与MC交于F.
已知:如图,在梯形ABCD中,AB∥CD,M是AB的中点,分别连接AC、BD、MD、MC,且AC与MD交于点E,DB与MC交于F.(1)求证:EF∥CD;
(2)若AB=a,CD=b,求EF的长.
分析 (1)根据AB∥CD,得到△AME∽△CDE,△BMF∽△CDF,于是得到$\frac{AM}{CD}=\frac{ME}{DE}$,$\frac{BM}{CD}=\frac{MF}{CF}$,等量代换得到$\frac{ME}{ED}=\frac{MF}{CF}$,然后根据平行线分线段成比例定理即可得到论;
(2)由(1)证得$\frac{AM}{CD}=\frac{ME}{DE}$,即$\frac{\frac{1}{2}a}{b}=\frac{ME}{DE}$,根据比例的性质得到$\frac{\frac{1}{2}a}{\frac{1}{2}a+b}=\frac{ME}{MD}$,然后根据平行线分线段成比例定理即可得到结论.
解答 解:(1)∵M是AB的中点,
∴AM=BM,
∵AB∥CD,
∴△AME∽△CDE,△BMF∽△CDF,
∴$\frac{AM}{CD}=\frac{ME}{DE}$,$\frac{BM}{CD}=\frac{MF}{CF}$,
∴$\frac{ME}{ED}=\frac{MF}{CF}$,
∴EF∥CD;
(2)由(1)证得$\frac{AM}{CD}=\frac{ME}{DE}$,∵AB=a,CD=b,
∴$\frac{\frac{1}{2}a}{b}=\frac{ME}{DE}$,
∴$\frac{\frac{1}{2}a}{\frac{1}{2}a+b}=\frac{ME}{MD}$,
∵EF∥CD,
∴$\frac{ME}{MD}=\frac{EF}{CD}$,
即:$\frac{EF}{b}=\frac{\frac{1}{2}a}{b+\frac{1}{2}a}$,
∴EF=$\frac{ab}{2b+a}$.
点评 本题考查了平行线分线段成比例,相似三角形的判定和性质,比例的性质,熟练掌握各定理是解题的关键.

| 方程 | 一般形式 | 二次项系数 | 一次项系数 | 常数项 |
| 4y2=5-3y | 4y2+3y-5=0 | 4 | 3 | -5 |
| (3x+1)2-2x=0 | 9x2+4x+1=0 | 9 | 4 | 1 |
| $\sqrt{3}{x}^{2}$+x2-2x=1 | ($\sqrt{3}$+1)x2-2x-1=0 | $\sqrt{3}$+1 | -2 | -1 |
| A. | x=2 | B. | x≠2 | C. | x≠-1 | D. | x≠0 |
 在△ABC中,点D、E、F分别在BC、AB、AC上,BE=CF,△DEB与△DFC的面积相等.求证:AD平分∠BAC.
在△ABC中,点D、E、F分别在BC、AB、AC上,BE=CF,△DEB与△DFC的面积相等.求证:AD平分∠BAC.