题目内容
8.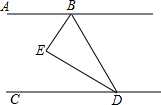 如图,已知AB∥CD,BE平分∠ABD,DE平分∠BDC,H是直线CD上一动点,(不与点D重合),BI平分∠HBD,写出∠EBI与∠BHD的数量关系,并说明理由.
如图,已知AB∥CD,BE平分∠ABD,DE平分∠BDC,H是直线CD上一动点,(不与点D重合),BI平分∠HBD,写出∠EBI与∠BHD的数量关系,并说明理由.
分析 根据角平分线的定义可得∠ABD=2∠EBD,∠HBD=2∠IBD,然后分点H在点D的左边和右边两种情况,表示出∠ABH和∠EBI,从而得解.
解答  解:∠BHD=2∠EBI或∠BHD=180°-2∠EBI.
解:∠BHD=2∠EBI或∠BHD=180°-2∠EBI.
理由:∵BE平分∠ABD,
∴∠ABD=2∠EBD,
∵BI平分∠HBD,
∴∠HBD=2∠IBD,
如图1,点H在点D的左边时,∠ABH=∠ABD-∠HBD,
∠EBI=∠EBD-∠IBD,
∴∠ABH=2∠EBI,
∵AB∥CD,
∴∠BHD=∠ABH,
∴∠BHD=2∠EBI;
如图2,点H在点D的右边时,∠ABH=∠ABD+∠HBD,
∠EBI=∠EBD+∠IBD,
∴∠ABH=2∠EBI,
∵AB∥CD,
∴∠BHD=180°-∠ABH,
∴∠BHD=180°-2∠EBI,
综上所述,∠BHD=2∠EBI或∠BHD=180°-2∠EBI.
点评 本题考查了平行线的性质,角平分线的定义,熟记性质是解题的关键,难点在于分情况讨论并理清图中各角度之间的关系.

练习册系列答案
相关题目
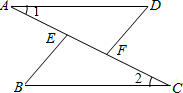 如图,已知点A、E、F、C在同一直线上,∠1=∠2,AE=CF,AD=CB.判断BE和DF的位置关系,并说明理由.
如图,已知点A、E、F、C在同一直线上,∠1=∠2,AE=CF,AD=CB.判断BE和DF的位置关系,并说明理由. 如图,已知正六边形ABCDEF内接于⊙O,且边长为4.
如图,已知正六边形ABCDEF内接于⊙O,且边长为4.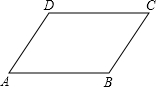 如图,AD∥BC,∠BAD=∠BCD,求证:AB∥CD.
如图,AD∥BC,∠BAD=∠BCD,求证:AB∥CD.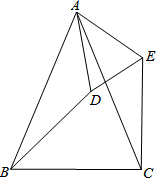 如图,△ABC和△ADE都是顶角为45°的等腰三角形,BC、DE分别是这两个等腰三角形的底边.图中的△ACE可以看成由哪个三角形通过怎样的旋转得到的?证明△ACE与这三角形全等.
如图,△ABC和△ADE都是顶角为45°的等腰三角形,BC、DE分别是这两个等腰三角形的底边.图中的△ACE可以看成由哪个三角形通过怎样的旋转得到的?证明△ACE与这三角形全等. 按要求完成下列问题:
按要求完成下列问题: