题目内容
 如图,用一段长为40米的篱笆围成一个一边靠墙的矩形菜园,墙长为22米.
如图,用一段长为40米的篱笆围成一个一边靠墙的矩形菜园,墙长为22米.(1)设矩形菜园的宽为x米,面积为y平方米,请写出y与x之间的函数关系式;
(2)当这个矩形的长、宽各为多少时,菜园的面积最大?最大面积是多少?
考点:二次函数的应用
专题:几何图形问题
分析:(1)先表示出矩形的长,再由矩形的面积公式就可以得出结论;
(2)将(1)的解析式转化为顶点式,由二次函数的性质就可以得出结论.
(2)将(1)的解析式转化为顶点式,由二次函数的性质就可以得出结论.
解答:解:(1)由题意,得
y=x(40-2x),
y=-2x2+40x.
答:y与x之间的函数关系式为y=-2x2+40x;
(2)∵y=-2x2+40x.
∴y=-2(x-10)2+200.
∴a=-2<0,
∴x=10时,y最大=200.
∴长为:40-2×10=20米.
答:这个矩形的长为20米,宽为10米时,菜园的面积最大,最大面积是200平方米.
y=x(40-2x),
y=-2x2+40x.
答:y与x之间的函数关系式为y=-2x2+40x;
(2)∵y=-2x2+40x.
∴y=-2(x-10)2+200.
∴a=-2<0,
∴x=10时,y最大=200.
∴长为:40-2×10=20米.
答:这个矩形的长为20米,宽为10米时,菜园的面积最大,最大面积是200平方米.
点评:本题考查了矩形的面积公式的运用,二次函数的解析式的运用,二次函数的顶点式的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是( )
A、 |
B、 |
C、 |
D、 |
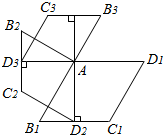 如图,菱形AB1C1D1的边长为1,∠B1=60°,作AD2⊥B1C1于点D2,以AD2为一边,作第二个菱形AB2C2D2,使∠B2=60°;作AD3⊥B2C2于点D2,以AD3为一边作第三个菱形AB3C3D3,使∠B3=60°…依此类推
如图,菱形AB1C1D1的边长为1,∠B1=60°,作AD2⊥B1C1于点D2,以AD2为一边,作第二个菱形AB2C2D2,使∠B2=60°;作AD3⊥B2C2于点D2,以AD3为一边作第三个菱形AB3C3D3,使∠B3=60°…依此类推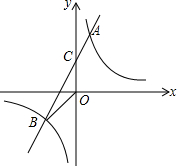 已知A(1,4),B(n,-2)是一次函数y=kx+b的图象和反比例函数y=
已知A(1,4),B(n,-2)是一次函数y=kx+b的图象和反比例函数y=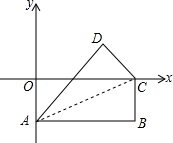 如图,在直角坐标系中,长方形OABC的边OA在y轴的负半轴上,边OC在x轴的正半轴上,点B的坐标为(8,-4),将长方形沿对角线AC翻折,点B落在点D的位置.那么点D的坐标是
如图,在直角坐标系中,长方形OABC的边OA在y轴的负半轴上,边OC在x轴的正半轴上,点B的坐标为(8,-4),将长方形沿对角线AC翻折,点B落在点D的位置.那么点D的坐标是 平行四边形ABCD,过C任意作一条直线交AB于E,BF⊥CE于点F,DG⊥CE于点G,AH⊥DG于点H,从图形中找出(不是平行四边形的一组对边的)两条相等的线段,并证明.
平行四边形ABCD,过C任意作一条直线交AB于E,BF⊥CE于点F,DG⊥CE于点G,AH⊥DG于点H,从图形中找出(不是平行四边形的一组对边的)两条相等的线段,并证明. 已知:如图,∠AOB是平角,∠AOD=40°.
已知:如图,∠AOB是平角,∠AOD=40°. 某容器内充满了一定质量的气体,当温度不变时,容器内气体的气压P(千帕)是气体体积V(立方米)的反比例函数,其图象如图所示.
某容器内充满了一定质量的气体,当温度不变时,容器内气体的气压P(千帕)是气体体积V(立方米)的反比例函数,其图象如图所示.