题目内容
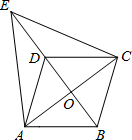 如图,在?ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC是等边三角形.
如图,在?ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC是等边三角形.(1)求证:四边形ABCD是菱形.
(2)若AC=8,AB=5,求ED的长.
考点:菱形的判定与性质,勾股定理,平行四边形的性质
专题:
分析:(1)根据平行四边形的性质得出AO=CO,根据等边三角形的性质得出EA=EC,推出EO⊥AC,根据菱形的判定得出即可;
(2)根据勾股定理求出BO,求出DO,根据勾股定理求出EO,即可得出答案.
(2)根据勾股定理求出BO,求出DO,根据勾股定理求出EO,即可得出答案.
解答:(1)证明:∵四边形ABCD是平行四边形,
∴AO=CO,
∵△EAC是等边三角形,
∴EA=EC,
∴EO⊥AC,
∴四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,AC=8,
∴AO=CO=4,DO=BO,
在Rt△ABO中,BO=
=3,
∴DO=BO=3,
在Rt△EAO中,EO=
=4
,
∴ED=EO-DO=4
-3.
∴AO=CO,
∵△EAC是等边三角形,
∴EA=EC,
∴EO⊥AC,
∴四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,AC=8,
∴AO=CO=4,DO=BO,
在Rt△ABO中,BO=
| AB2-AO2 |
∴DO=BO=3,
在Rt△EAO中,EO=
| EA2-AO2 |
| 3 |
∴ED=EO-DO=4
| 3 |
点评:本题考查了菱形的性质和判定,勾股定理,等腰三角形的性质,平行四边形的性质,等边三角形的性质的应用,能综合运用性质进行推理是解此题的关键,综合性比较强,有一定的难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
观察下面由正整数组成的数阵:

照此规律,按从上到下、从左到右的顺序,第50行的第50个数是( )

照此规律,按从上到下、从左到右的顺序,第50行的第50个数是( )
| A、2450 | B、2451 |
| C、2550 | D、2551 |
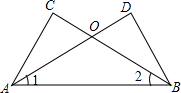 已知:如图,∠1=∠2,∠C=∠D.求证:
已知:如图,∠1=∠2,∠C=∠D.求证: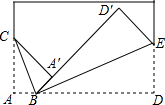 如图,将长方形纸片的一角折叠,使顶点A落在点A′处,折痕CB;再将长方形纸片的另一角折叠,使顶点D落在点D′处,D′在BA′的延长线上,折痕EB.
如图,将长方形纸片的一角折叠,使顶点A落在点A′处,折痕CB;再将长方形纸片的另一角折叠,使顶点D落在点D′处,D′在BA′的延长线上,折痕EB.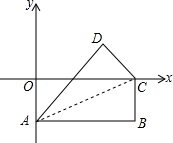 如图,在直角坐标系中,长方形OABC的边OA在y轴的负半轴上,边OC在x轴的正半轴上,点B的坐标为(8,-4),将长方形沿对角线AC翻折,点B落在点D的位置.那么点D的坐标是
如图,在直角坐标系中,长方形OABC的边OA在y轴的负半轴上,边OC在x轴的正半轴上,点B的坐标为(8,-4),将长方形沿对角线AC翻折,点B落在点D的位置.那么点D的坐标是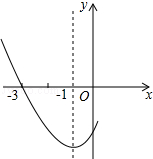 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=-1,且过点(-3,0),下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(3,y2)是抛物线上两点,则y1<y2,其中说法正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=-1,且过点(-3,0),下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(3,y2)是抛物线上两点,则y1<y2,其中说法正确的是( ) 已知:如图,∠AOB是平角,∠AOD=40°.
已知:如图,∠AOB是平角,∠AOD=40°. 如图,作出△ABC绕点C逆时针旋转60°的图形.
如图,作出△ABC绕点C逆时针旋转60°的图形.