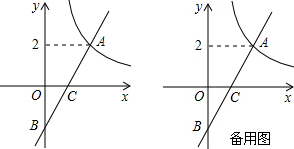题目内容
3. 2015“两相和”杯群星演唱会在我市体育馆进行,市文化局、广电局
2015“两相和”杯群星演唱会在我市体育馆进行,市文化局、广电局在策划本次活动,在与单位协商团购票时推出两种方案.设购买门票数为x(张),总费用为y(元).
方案一:若单位赞助广告费8000元,则该单位所购门票的价格为每张50元;(总费用=广告赞助费+门票费)
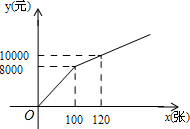
方案二:直接购买门票方式如图所示.
解答下列问题:
(1)方案一中,y与x的函数关系式为y=8000+50x;
方案二中,当0≤x≤100时,y与x的函数关系式为y=80x,
当x>100时,y与x的函数关系式为y=100x-2000;
(2)甲、乙两单位分别采用方案一、方案二购买本场演唱会门票共700张,花去总费用计56000元,求甲、乙两单位各购买门票多少张?
分析 (1)方案一中,总费用=广告赞助费8000+门票单价50×票的张数;
方案二中,当0≤x≤100时,应先算出门票的单价,进而乘以张数即可;
当x>100时,设出一次函数解析式,把其中两点的坐标代入即可求得相应的函数解析式;
(2)设甲单位购买了a张门票,则乙单位购买了(700-a)张门票,进而根据票价为56000元,分乙单位没有超过100张票及超过100张票两种情况进行探讨,找到合适的解即可.
解答 解:(1)方案一:单位赞助广告费8000元,该单位所购门票的价格为每张50元,则y=8000+50x;
方案二:当0≤x≤100时,门票单价为8000÷100=80元,则y=80x;
当x>100时,设解析式为y=kx+b.
将(100,8000),(120,10000)代入,
得$\left\{\begin{array}{l}{100k+b=8000}\\{120k+b=10000}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=100}\\{b=-2000}\end{array}\right.$,
所以y=100x-2000.
故答案为y=8000+50x;y=80x;y=100x-2000;
(2)设甲单位购买了a张门票,则乙单位购买了(700-a)张门票.
①当0≤700-a≤100时,
8000+50a+80(700-a)=56000,
解得a=266$\frac{2}{3}$(不合题意,舍去);
②当700-a>100时,
8000+50a+100(700-a)-2000=56000,
解得a=400,
则700-a=300.
答:甲单位购买门票400张,乙单位购买门票300张.
点评 本题考查了一次函数的应用,待定系数法求一次函数的解析式的运用,及一元一次方程解决实际问题的运用,在解答的过程中求出一次函数的解析式y=100x-2000是解答全题的关键,根据自变量不同的取值,对总门票费分情况进行探讨是解决本题的易错点.

 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
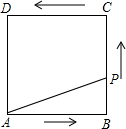 如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→B→C→D→A,设P点经过的路程为x,以点A,P,B为顶点的三角形的面积是y,则下列图象能大致描述y与x的函数关系的是( )
如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→B→C→D→A,设P点经过的路程为x,以点A,P,B为顶点的三角形的面积是y,则下列图象能大致描述y与x的函数关系的是( )| A. | 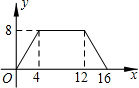 | B. | 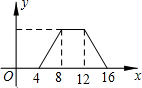 | C. | 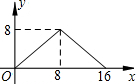 | D. | 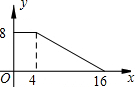 |
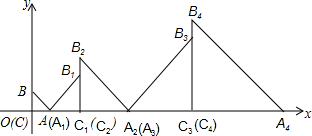
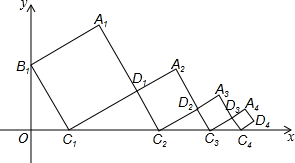 如图,平面直角坐标系中放置了四个正方形,其中相邻两个正方形的两边在同一直线上,已知正方形A1B1C1D1的边长为1,∠OC1B1=60°.若按此规律排列,第2015个小正方形最上面的顶点A2015的纵坐标是( )
如图,平面直角坐标系中放置了四个正方形,其中相邻两个正方形的两边在同一直线上,已知正方形A1B1C1D1的边长为1,∠OC1B1=60°.若按此规律排列,第2015个小正方形最上面的顶点A2015的纵坐标是( )| A. | ($\frac{\sqrt{3}}{3}$)2014×($\frac{1+\sqrt{3}}{2}$) | B. | ($\frac{\sqrt{3}}{3}$)2015($\frac{1+\sqrt{3}}{2}$) | C. | ($\frac{\sqrt{3}}{2}$)2014×($\frac{1+\sqrt{3}}{3}$) | D. | ($\frac{\sqrt{3}}{2}$)2015×($\frac{1+\sqrt{3}}{3}$) |
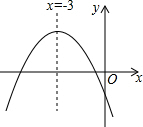 二次函数y=ax2+bx+c的图象如图所示,已知A(-1,y),B(-4,y2)和C(-5,y3)都在此图象上,下列关系式正确的是( )
二次函数y=ax2+bx+c的图象如图所示,已知A(-1,y),B(-4,y2)和C(-5,y3)都在此图象上,下列关系式正确的是( )| A. | y1<y3<y2 | B. | y1>y2>y3 | C. | y3<y2=y1 | D. | y1=y3<y2 |