题目内容
12.如图,在平面直角坐标系中,Rt△ABC的直角顶点C与原点O重合,直角边AC,BC分别在x轴和y轴的正半轴上,且长度分别为3和4,Rt△A1B1C1,Rt△A2B2C2,Rt△A3B3C3,Rt△A4B4C4…按照如图所示的规律排列,均为Rt△ABC相似,且A1B1=10,A2B2=15,A3B3=20,A4B4=25…,则A100的坐标为(15453,0).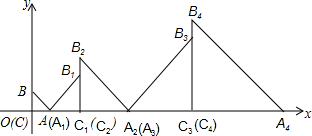
分析 根据相似计算出A、A1、A2、A3、A4、A5、A6、A7的坐标,找出规律,即可得到A100的坐标.
解答 解:∵直角边AC,BC分别在x轴和y轴的正半轴上,且长度分别为3和4,
∴AB=5,
∵Rt△A1B1C1,Rt△A2B2C2,Rt△A3B3C3,Rt△A4B4C4…均与Rt△ABC相似,
∵AB=5,A1B1=10,A2B2=15,A3B3=20,A4B4=25…,
∴OA1=3=3×1,OA2=OA3=3+6+9=3(1+2+3),OA4=OA5=3+6+9+12+15=3(1+2+3+4+5),…,
以依此规律,
∴OA100=OA101=3(1+2+3+4+5+…+101)=15453,
∴A100的坐标为:(15453,0).
故答案为:(15453,0).
点评 本题考查了三角形相似和图形变化规律,根据相似三角形的性质计算出出A、A1、A2、A3、A4、A5、A6、A7的坐标,发现规律是解决问题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
2.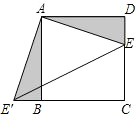 如图,在正方形ABCD中,AB=3,点E在CD边上,DE=1,把△ADE绕点A顺时针旋转90°,得到△ABE′,连接EE′,则线段EE′的长为( )
如图,在正方形ABCD中,AB=3,点E在CD边上,DE=1,把△ADE绕点A顺时针旋转90°,得到△ABE′,连接EE′,则线段EE′的长为( )
 如图,在正方形ABCD中,AB=3,点E在CD边上,DE=1,把△ADE绕点A顺时针旋转90°,得到△ABE′,连接EE′,则线段EE′的长为( )
如图,在正方形ABCD中,AB=3,点E在CD边上,DE=1,把△ADE绕点A顺时针旋转90°,得到△ABE′,连接EE′,则线段EE′的长为( )| A. | $2\sqrt{5}$ | B. | $2\sqrt{3}$ | C. | 4 | D. | $2\sqrt{10}$ |
 2015“两相和”杯群星演唱会在我市体育馆进行,市文化局、广电局
2015“两相和”杯群星演唱会在我市体育馆进行,市文化局、广电局
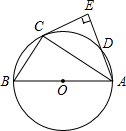 如图,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,且∠BAC=∠CAD,过点C作CE⊥AD,垂足为点E.
如图,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,且∠BAC=∠CAD,过点C作CE⊥AD,垂足为点E.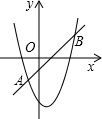 如图,抛物线y1=x2+mx+n与直线y2=x-1交于点A(a,-2)和B(b,2).
如图,抛物线y1=x2+mx+n与直线y2=x-1交于点A(a,-2)和B(b,2).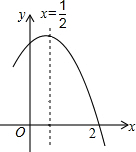 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=$\frac{1}{2}$,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=$\frac{1}{2}$,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )