题目内容
18．如图，在平面直角坐标系xOy中，函数y=$\frac{4}{x}$（x＞0）的图象与一次函数y=kx-k的图象交点为A（m，2）．（1）求一次函数的解析式；
（2）写出反比例函数值大于一次函数值时x的取值范围；
（3）设一次函数y=kx-k的图象与y轴交于点B，若P是x轴上一点，且满足△PAB的面积是4，求P的坐标．
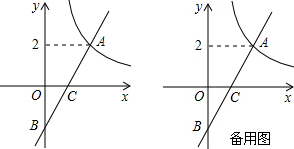
分析 （1）将A点坐标代入y=$\frac{4}{x}$（x＞0），求出m的值为2，再将（2，2）代入y=kx-k，求出k的值，即可得到一次函数的解析式；
（2）根据图象即可求得；
（3）将三角形以x轴为分界线，分为两个三角形计算，再把它们相加．
解答 解：（1）将A（m，2）代入y=$\frac{4}{x}$（x＞0）得，
m=2，
则A点坐标为A（2，2），
将A（2，2）代入y=kx-k得，2k-k=2，
解得k=2，则一次函数解析式为y=2x-2；
（2）∵A（2，2），
∴根据图象可知：反比例函数值大于一次函数值时x的取值范围0＜x＜2；
（3）∵一次函数y=2x-2与x轴的交点为C（1，0），与y轴的交点为B（0，-2），
S△ABP=S△ACP+S△BPC，
∴$\frac{1}{2}$×2CP+$\frac{1}{2}$×2CP=4，
解得CP=2．
则P点坐标为（3，0），（-1，0）．
点评 本题考查了反比例函数与一次函数的交点问题，求出函数解析式并熟悉点的坐标与图形的关系是解题的关键．
练习册系列答案
相关题目
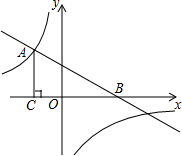如图，一次函数y=-$\frac{1}{2}$x+2的图象与x轴交于点B，与反比例函数y=$\frac{m}{x}$的图象的交点为A（-2，3）．
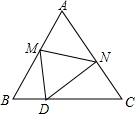如图，在等边三角形纸片△ABC中，将纸片折叠，点A落在BC边上的点D处，MN为折痕，当DN⊥NC时，CN=1，则A、D两点之间的距离为$\sqrt{6}$．
如图，△ABC中，DE∥BC，DE=2，AD=3，DB=4，则BC的长是$\frac{14}{3}$．
2015“两相和”杯群星演唱会在我市体育馆进行，市文化局、广电局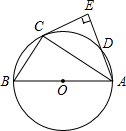
如图，△ABC内接于⊙O，AB是⊙O的直径，点D在⊙O上，且∠BAC=∠CAD，过点C作CE⊥AD，垂足为点E．
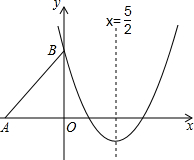如图，Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，O为坐标原点，A、B两点的坐标分别为（-3，0）、（0，4），抛物线y=$\frac{2}{3}$x2+bx+c经过点B，且顶点在直线x=$\frac{5}{2}$上．