题目内容
3.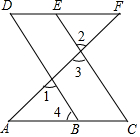 如图,∠1=∠2,∠C=∠D,
如图,∠1=∠2,∠C=∠D,(1)求证:BD∥CE.
(2)求证:∠A=∠F.
分析 (1)根据已知条件得到∠1=∠3,根据平行线的判定定理即可得到结论;
(2)根据平行线的性质得到∠4=∠C,等量代换得到∠4=∠D,于是得到FD∥CA,根据平行线的性质即可得到结论.
解答 证明:(1)∵∠3=∠2,∠1=∠2,
∴∠1=∠3,
∴BD∥CE;
(2)∵BD∥CE,
∴∠4=∠C,
∵∠C=∠D,
∴∠4=∠D,
∴FD∥CA,
∴∠A=∠F.
点评 本题主要考查平行线的性质和判定,熟练运用平行线的性质和判定是解决此类问题的关键.解决此题的关键是善于发现图形中的隐含条件.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
13.已知$\sqrt{{x}^{2}}$=5,则x为( )
| A. | 5 | B. | -5 | C. | ±5 | D. | 以上都不对 |
18.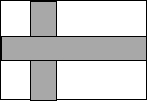 如图,大矩形长是10厘米,宽是8厘米,阴影部分宽为2厘米,则空白部分面积是( )
如图,大矩形长是10厘米,宽是8厘米,阴影部分宽为2厘米,则空白部分面积是( )
 如图,大矩形长是10厘米,宽是8厘米,阴影部分宽为2厘米,则空白部分面积是( )
如图,大矩形长是10厘米,宽是8厘米,阴影部分宽为2厘米,则空白部分面积是( )| A. | 36平方厘米 | B. | 40平方厘米 | C. | 32平方厘米 | D. | 48平方厘米 |
8.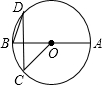 如图,已知A,B,C,D是⊙O上的点,AB⊥CD,OA=2,CD=2$\sqrt{3}$,则∠D等于( )
如图,已知A,B,C,D是⊙O上的点,AB⊥CD,OA=2,CD=2$\sqrt{3}$,则∠D等于( )
 如图,已知A,B,C,D是⊙O上的点,AB⊥CD,OA=2,CD=2$\sqrt{3}$,则∠D等于( )
如图,已知A,B,C,D是⊙O上的点,AB⊥CD,OA=2,CD=2$\sqrt{3}$,则∠D等于( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |

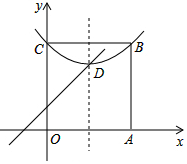 如图,抛物线y=m(x-s)2+3经过正方形OABC的两个顶点B、C,且抛物线顶点D在正方形OABC内部.
如图,抛物线y=m(x-s)2+3经过正方形OABC的两个顶点B、C,且抛物线顶点D在正方形OABC内部.