题目内容
8.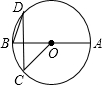 如图,已知A,B,C,D是⊙O上的点,AB⊥CD,OA=2,CD=2$\sqrt{3}$,则∠D等于( )
如图,已知A,B,C,D是⊙O上的点,AB⊥CD,OA=2,CD=2$\sqrt{3}$,则∠D等于( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
分析 首先依据垂径定理得到CE的长,然后利用特殊锐角三角函数值可求得∠EOC的度数,最后,利用圆周角定理求解即可.
解答 解:如图所示:
∵AB⊥CD,CD=2$\sqrt{3}$,
∴CE=$\sqrt{3}$.
在Rt△OCE中,OC=OA=2,CE=$\sqrt{3}$,
∴∠EOC=60°,
∴∠D=30°.
故选:C.
点评 本题主要考查的是垂径定理、圆周角定理、特殊锐角三角函数值的应用,熟练掌握相关知识是解题的关键.

练习册系列答案
相关题目
16.某瓶中装有1分,2分,5分三种硬币,15枚硬币共3角5分,则有多少种装法( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.某地夏天的最低气温是13℃,最高气温是30℃,则这天气温是t(℃)的取值范围是( )
| A. | t<13 | B. | t>30 | C. | 13<t<30 | D. | 13≤t≤30 |
 如图,某地进行城市规划,在一条新修 公路旁有一超市,现要建一个汽车站.为了超市距离车站最近,请你在公路上选一点来建汽车站,应建在( )
如图,某地进行城市规划,在一条新修 公路旁有一超市,现要建一个汽车站.为了超市距离车站最近,请你在公路上选一点来建汽车站,应建在( )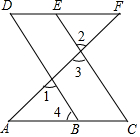 如图,∠1=∠2,∠C=∠D,
如图,∠1=∠2,∠C=∠D, 如图,∠1+∠2=180°,∠3=108°.
如图,∠1+∠2=180°,∠3=108°.