题目内容
11.已知∠AOB=120°,射线OC、OD在∠AOB内部,∠COD=40°.
(1)如图1,若OM平分∠AOC,ON平分∠BOD,求∠MON的度数;
(2)如图2,若OM平分∠AOD,ON平分∠BOC,求∠MON的度数;
(3)在(2)的条件下,若∠DON与∠BON的度数比为1:5,求∠AOC与∠DOM的度数比.
分析 (1)根据角平分线的定义和角的和差即可得到结论;
(2)根据角平分线的定义和角的和差即可得到结论;
(3)根据已知条件列方程即可得到结论.
解答 解:(1)∵OM平分∠AOC,ON平分∠BOD,
∴∠COM=$\frac{1}{2}$∠AOC,∠DON=$\frac{1}{2}$∠BOD,
∴∠MON=∠MOC+∠COD+∠DON
=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOD+∠COD
=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOD+$\frac{1}{2}$∠COD+$\frac{1}{2}$∠COD
=$\frac{1}{2}$(∠AOC+∠BOD+∠COD)+$\frac{1}{2}$∠COD
=$\frac{1}{2}$∠AOB+$\frac{1}{2}$∠COD
∵∠AOB=120°,∠COD=40°,
∴∠MON=60°+20°=80°.
(2)∵OM平分∠AOD,ON平分∠BOC,
∴∠AOD=2∠DOM、∠BOC=2∠NOC,
又∵∠AOB=∠AOD+∠BOC-∠COD,
∴∠AOB=2∠DOM+2∠NOC-∠COD,
即∠AOB=2(∠DOM+∠NOC)-∠COD,
∵∠AOB=120°、∠COD=40°,
∴∠DOM+∠NOC=80°,
则∠MON=∠DOM+∠NOC-∠COD=40°;
(3)∵∠DON与∠BON的度数比为1:5,
∴设∠DON=α,∠BON=5α,
∴∠CON=∠BON=5α,
∴∠COD=4α=40°,
∴α=10°,
∴∠DON=10°,
∵∠MON=∠COD=40°,
∴∠COM=∠DON=10°,
∴∠DOM=∠MON-∠DON=30°,
∴∠AOM=∠DOM=30°,
∴∠AOC=20°.
点评 本题考查了角度的计算,角平分线的定义,正确的识别图形是解题的关键.

| A. | x2-1=x2 | B. | ax2+bx+c=0 | C. | x2-x-2=0 | D. | x2+y=1 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图,菱形ABCD的周长为48cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长等于6cm.
如图,菱形ABCD的周长为48cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长等于6cm. 如图,某地进行城市规划,在一条新修 公路旁有一超市,现要建一个汽车站.为了超市距离车站最近,请你在公路上选一点来建汽车站,应建在( )
如图,某地进行城市规划,在一条新修 公路旁有一超市,现要建一个汽车站.为了超市距离车站最近,请你在公路上选一点来建汽车站,应建在( ) 如图,在△ABC中,BD,CE分别为AC,AB边上的中线,BD⊥CE.若BD=3,CE=2,则△ABC的面积为( )
如图,在△ABC中,BD,CE分别为AC,AB边上的中线,BD⊥CE.若BD=3,CE=2,则△ABC的面积为( )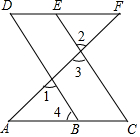 如图,∠1=∠2,∠C=∠D,
如图,∠1=∠2,∠C=∠D, 如图,∠1+∠2=180°,∠3=108°.
如图,∠1+∠2=180°,∠3=108°. 如图,AB和CD相交于点O,∠C=∠COA,∠D=∠BOD.
如图,AB和CD相交于点O,∠C=∠COA,∠D=∠BOD.