题目内容
14.已知x=$\sqrt{2}$+1,y=$\sqrt{2}$-1,求下列各式的值.(1)x2-2xy+y2;
(2)x2+y2.
分析 (1)首先判断出x2-2xy+y2=(x-y)2,然后把x=$\sqrt{2}$+1,y=$\sqrt{2}$-1代入,求出算式x2-2xy+y2的值是多少即可.
(2)把x=$\sqrt{2}$+1,y=$\sqrt{2}$-1代入x2+y2,求出算式的值是多少即可.
解答 解:(1)x2-2xy+y2
=(x-y)2
=${[(\sqrt{2}+1)-(\sqrt{2}-1)]}^{2}$
=22
=4
(2)x2+y2
=($\sqrt{2}+1$)2+($\sqrt{2}-1$)2
=3$+2\sqrt{2}+3-2\sqrt{2}$
=6
点评 此题主要考查了二次根式的化简求值,要熟练掌握,解答此题的关键是要明确化简二次根式的步骤:①把被开方数分解因式;②利用积的算术平方根的性质,把被开方数中能开得尽方的因数(或因式)都开出来;③化简后的二次根式中的被开方数中每一个因数(或因式)的指数都小于根指数2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.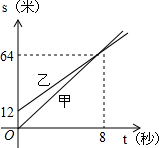 如图是表示的是甲、乙两名同学运动的图象,图中s和t分别表示运动的路程和时间,根据图象判断,快者的速度比慢者的速度每秒快( )
如图是表示的是甲、乙两名同学运动的图象,图中s和t分别表示运动的路程和时间,根据图象判断,快者的速度比慢者的速度每秒快( )
 如图是表示的是甲、乙两名同学运动的图象,图中s和t分别表示运动的路程和时间,根据图象判断,快者的速度比慢者的速度每秒快( )
如图是表示的是甲、乙两名同学运动的图象,图中s和t分别表示运动的路程和时间,根据图象判断,快者的速度比慢者的速度每秒快( )| A. | 2.5米 | B. | 2米 | C. | 1.5米 | D. | 1米 |
19.为了加速内蒙古经济建设,国家计划投资204.4亿元修建赤峰市至喀左的“高铁”,204.4亿用科学记数法表示正确的是( )
| A. | 0.2044×1011 | B. | 20.44×109 | C. | 2.044×108 | D. | 2.044×1010 |