��Ŀ����
1������ѧϰ�У��Ա���ȡֵ��Χ����Ӧ�ĺ���ֵ��Χ�����Ǵ�ҹ�ע���ص�֮һ��������������⣮��1���ֱ������2��x��4ʱ������������y=2x+1��y=$\frac{2}{x}$��y=2��x-1��2+1�����ֵ����Сֵ��
��2����y=$\frac{2}{x}$��ֵ������2�������������x�ķ�Χ��
��3����y=$\frac{k}{x}$����a��x��2ʱ�������ֵ��������Сֵ����a��ȡֵ��Χ��
��4��y=2��x-m��2+m-2����2��x��4ʱ����СֵΪ1����m��ֵ��
���� ��1������k=2��0���һ�κ��������ʼ��ɵó�����2��x��4ʱ��y=2x+1�����ֵ����Сֵ�����ݶ��κ����Ľ���ʽ��϶��κ��������ʼ��ɵó�����2��x��4ʱ��y=2��x-1��2+1�����ֵ����Сֵ��
��2����y=$\frac{2}{x}$��2����֮���ɵó�x��ȡֵ��Χ��
��3���ٵ�k��0ʱ����ͼ�õ�0��x��2ʱ���õ�y=$\frac{k}{2}$�����ֵ������Сֵ$\frac{k}{2}$��ͬ����a��0ʱ����a��x��0ʱ���õ�y��$\frac{k}{a}$�����ֵ$\frac{k}{a}$������Сֵ���ڵ�k��0ʱ����ͼ�õ�0��x��2ʱ��y=$\frac{k}{2}$����Сֵ�������ֵ$\frac{k}{2}$��ͬ����a��0ʱ����a��x��0ʱ��y��$\frac{k}{a}$����Сֵ$\frac{k}{a}$�������ֵ�����ǵõ����ۣ�
��4����m��2��2��m��4��m��4����������ǣ����ݶ��κ��������ʽ�ϵ�2��x��4ʱ����СֵΪ1���ɵó�����m��һԪ���η��̣�һԪһ�η��̣�����֮���ɵó����ۣ�
���  �⣺��1����y=2x+1��k=2��0��
�⣺��1����y=2x+1��k=2��0��
��y��x�����������
�൱x=2ʱ��y��С=5����x=4ʱ��y���=9��
��y=$\frac{2}{x}$��k=2��0��
����2��x��4��y��x�����������
�൱x=2ʱ��y���=1����x=4ʱ��y��С=$\frac{1}{2}$��
��y=2��x-1��2+1��a=2��0���������ߵĶԳ���Ϊx=1��
�൱x=1ʱ��y��С=1����x=4ʱ��y���=19��
��2����y=$\frac{2}{x}$��2��
��ã�x��0��x��1��
�����������x�ķ�ΧΪx��0��x��1��
��3���ٵ�k��0ʱ����ͼ�õ�0��x��2ʱ��y=$\frac{k}{2}$�����ֵ������Сֵ$\frac{k}{2}$��ͬ����a��0ʱ����a��x��0ʱ��y��$\frac{k}{a}$�����ֵ$\frac{k}{a}$������Сֵ���ڵ�k��0ʱ����ͼ�õ�0��x��2ʱ��y=$\frac{k}{2}$����Сֵ�������ֵ$\frac{k}{2}$��ͬ����a��0ʱ����a��x��0ʱ��y��$\frac{k}{a}$����Сֵ$\frac{k}{a}$�������ֵ���൱k��0��a��0ʱ����ʱ��y=$\frac{k}{x}$�������ֵ��������Сֵ������������a��ȡֵ��Χ��a��0��
��4���ٵ�m��2ʱ����2��2-m��2+m-2=1��
��ã�m1=1��m2=$\frac{5}{2}$����ȥ����
�ڵ�2��m��4ʱ����m-2=1��
��ã�m3=3��
�۵�m��4ʱ����2��4-m��2+m-2=1��
�����ã�2m2-15m+29=0��
�ߡ�=��-15��2-4��2��29=-7���⣮
��m��ֵΪ1��3��
�ٵ�k��0ʱ����ͼ�õ�0��x��2ʱ��y=$\frac{k}{2}$�����ֵ������Сֵ$\frac{k}{2}$��ͬ����a��0ʱ����a��x��0ʱ��y��$\frac{k}{a}$�����ֵ$\frac{k}{a}$������Сֵ���ڵ�k��0ʱ����ͼ�õ�0��x��2ʱ��y=$\frac{k}{2}$����Сֵ�������ֵ$\frac{k}{2}$��ͬ����a��0ʱ����a��x��0ʱ��y��$\frac{k}{a}$����Сֵ$\frac{k}{a}$�������ֵ���൱k��0��a��0ʱ����ʱ��y=$\frac{k}{x}$�������ֵ��������Сֵ������������a��ȡֵ��Χ��a��0��
���� ���⿼���˷��������������ʡ�һ�κ��������ʡ����κ����������Լ������б�ʽ������Ĺؼ��ǣ���1������һ�Σ����Σ����������ʽ����ֵ���⣻��2���ҳ�����x�IJ���ʽ����3����m��2��2��m��4��m��4����������ǣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�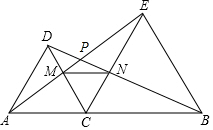 ��ͼ����CΪ�߶�AB��һ�㣬��DAC����ECB���ǵȱ������Σ�AE��DC���ڵ�M��DB��EC���ڵ�N��DB��AE���ڵ�P������MN������˵����ȷ�ĸ����У�������
��ͼ����CΪ�߶�AB��һ�㣬��DAC����ECB���ǵȱ������Σ�AE��DC���ڵ�M��DB��EC���ڵ�N��DB��AE���ڵ�P������MN������˵����ȷ�ĸ����У���������MN��AB���ڡ�DPM=60�㣻�ۡ�DAP=��PEC���ܡ�ACM�ա�DCN��������DBE=30�㣬���AEB=80�㣮
| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
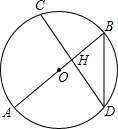 ��ͼ��AB�ǡ�O��ֱ������CD��AB��H����CD=2$\sqrt{2}$��BD=$\sqrt{3}$����AB�ij�Ϊ��������
��ͼ��AB�ǡ�O��ֱ������CD��AB��H����CD=2$\sqrt{2}$��BD=$\sqrt{3}$����AB�ij�Ϊ��������| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
| A�� | ����7��20�� | B�� | ����8��20�� | C�� | ����7��40�� | D�� | ����8��40�� |
| A�� | -2 | B�� | 2 | C�� | $\frac{1}{2}$ | D�� | -$\frac{1}{2}$ |
| A�� | $\sqrt{{2^2}+{7^2}}$=2+7 | B�� | $\sqrt{9\frac{1}{2}}$=3$\sqrt{\frac{1}{2}}$ | C�� | $\sqrt{6}$��$\sqrt{3}$=$\sqrt{2}$ | D�� | $\frac{{\sqrt{8}+\sqrt{12}}}{{\sqrt{2}}}$=4+6 |



